個別の因子の寄与率

寄与率のページに、一般的な重回帰分析で扱うデータの場合、モデル式の寄与率を求めることはできても、モデル式に入っている個別の因子の寄与率を調べることはできない話をしています。

寄与率を正確に計算できる場合

上記で、「一般的な重回帰分析で扱うデータの場合」の話をしていますが、変数が独立している場合は、個別の因子の寄与率を計算できます。

独立していると、下記のようなグラフと式が成り立つので、個別の因子の寄与率を計算できます。

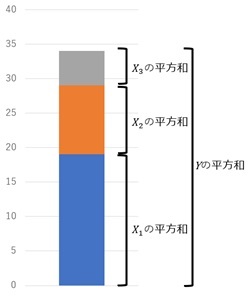
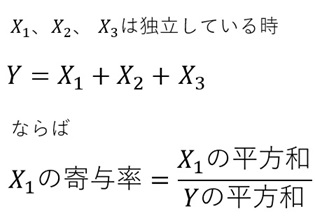
ANOVA ANOVA

寄与率を求めるには、因子が独立している必要があります。実験計画法で計画して集めたデータなら、このようなデータになります。

変数が独立しているように集めたデータの場合、重回帰分析を使うと、寄与率が求められます。

ここで、分母は、Yの平方和です。分子は、各説明変数の平方和ではなく、各説明変数の値に、重回帰分析の係数をかけた値の平方和です。重回帰分析の係数をかけた値が、上の式のX1に相当します。

説明変数同士が独立しているのなら、相関係数を使っても、寄与率が求まります。

Yと説明変数のひとつずつについて、相関係数の２乗を計算すると、それが寄与率になります。

標準偏回帰係数の２乗でも同じ計算ができます。

一般的なデータ分析では、既にあるデータを使うことが多いです。

一般的なデータでは、因子は独立していないのが普通なので、寄与率が計算できないです。

YがXの線形和で表せない場合は、上の式が成り立たないので、寄与率が計算できないです。

例えば、誤差の伝播があるような説明変数の関係がある場合が、これに当てはまります。

主成分を説明変数にした重回帰分析は、主成分回帰分析と言います。

主成分は、無相関になるように求まります。そのため、各変数の寄与が線形和としてYに表れている場合なら、主成分回帰分析で、各主成分の寄与率を求めることができます。

元になっている説明変数が、目的変数に対してどれだけの寄与をしているのかを直接求めることはできません。しかし、例えば、「主成分１と、説明変数Aはほぼ同じ意味」ということなら、主成分１の寄与率を、説明変数Aの寄与率として使えます。

主成分回帰分析では、寄与率が４種類あり、使い分けます。

Rによる主成分回帰分析では、４種類すべてが登場します。

主成分回帰分析では、目的変数を除いた、説明変数全部について、まず、主成分分析をして、主成分を求めます。主成分関係の寄与率が２種類あります。

この時に、「寄与率」が出ますが、これは、説明変数全体の多次元的なばらつきに対しての、各主成分の寄与率です。そのため、目的変数とは関係のない寄与率です。

また、各変数についての、各主成分の寄与率が、因子負荷量から求められます。話がややこしくなりますが、主成分は無相関なので、各変数と主成分の間には、上記の「寄与率を正確に計算できる場合」が成り立っています。

主成分回帰分析では、重回帰分析をするので、モデル式の目的変数に対する寄与率が求まります。

主成分回帰分析では、個別の因子の寄与率も求まります。

これは、各主成分の目的変数のばらつきに対しての寄与率です。