回帰分析 （ 単回帰分析 ）では、 傾き（回帰係数）と相関係数は、別のものとして勉強しますし、 使い道も違うものと思うのが普通です。
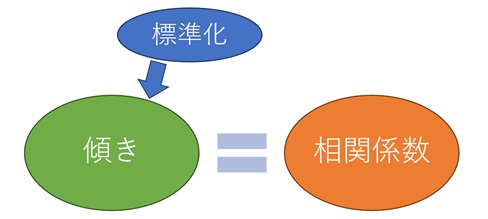
標準化 されたデータの回帰分析では、ちょっと不思議な事が起きます。
「 標準化 」と呼ばれるデータの換算の方法があります。 標準化をされた変数は、平均値が0、標準偏差が1になります。
XとYのそれぞれを標準化してから回帰分析します。
すると、傾きと相関係数の値が同じになります。
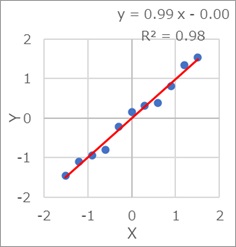
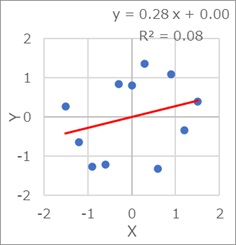
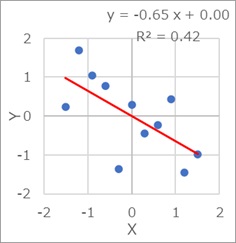
相関が弱ければ、傾きが小さくなります。 相関が強ければ、プラス側やマイナス側への傾きが大きくなります。
ただし、傾きの絶対値は、１（45度の線）が最大です。
X軸と区別がつかないくらい傾きが小さくなることはありますが、Y軸と区別がつなないくらい傾きが大きくなることはないです。
標準化されたデータの場合、傾きと相関係数が同じになるので、傾きの2乗は、 寄与率 としての意味を持ちます。
標準偏回帰係数 は、標準化したデータの場合の、 重回帰分析 の偏回帰係数です。
「いつでも」ではないのですが、偏回帰係数の2乗は、説明変数の寄与率として使うことができます。
順路
次は
曲線の回帰分析
