曲線の回帰分析

Yが1個、Xが1個の回帰分析は、単回帰分析と呼ばれます。XとYのデータが、
Y = A * X + B
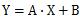
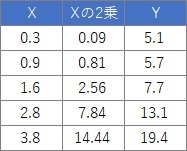
の式で表せると仮定します。

これだけでも役に立つ場面はいろいろあるのですが、上の式が表すのは直線です。「曲線の時にどうするのか？」、というのが、このページになります。

単回帰分析の式がそのまま使える場合

例えば、
Y = A * X + B
のようなデータがあったとします。直線でも良さそうですが、２次曲線に見えます。

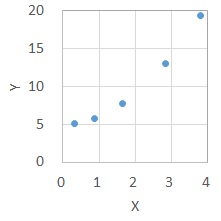
この時は、データにXを2乗した列を作ります。
Y = A * X + B

そして、「Xの2乗」を
Y = A * X + B
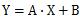
の「X」にいれて、単回帰分析をします。これだけです。

散布図を描く時は「X」の列と「Y」の列を使いますが、単回帰分析は「Xの2乗」と「Y」の列を使い、使い分けるのがポイントです。

このページの例は、2乗なので単純な曲線しか表せませんが、sin(X)などを使えば、もっと複雑なものも作れます。

上の式は、２次曲線でしたが、曲線の底がちょうとX=0の時の曲線になります。一般的な２次曲線の式は、
Y = A * X + B
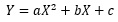
です。

この式を回帰分析で扱うときは、重回帰分析になります。データはXとYが1個ずつなのですが、数式の中の説明変数は複数なところがポイントです。一般的に単回帰分析は直線を表し、重回帰分析は平面や超平面を表現する式として使う方法として紹介されますが、ここでは、重回帰分析を曲線に使っています。

Xの2乗の列と、Xの列の2つを説明変数として重回帰分析をします。

散布図を描く時は「X」の列と「Y」の列を使うのは同じです。

説明変数の列を増やしたり、関数をいろいろ作ることで、いろいろな曲線を表すことができるようになります。