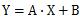___"1"It is called "linear function". If B is 0, the line is through original point.
Data Science likes the method with line for the analysis. One of the methods is correlation .
The function for a line is
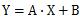___"1"
It is called "linear function".
If B is 0, the line is through original point.
If the number of X is "n",
___"2"
This is also called a linear function.
If we write the phenomenon with this function, we call "there is linearity".
The functions "1" and "2" are used in multi-regression analysis .
The regression analysis to make "1" is "linear single regression analysis". That for "2" is "linear multi regression analysis".
Linear-approximation is the method that uses linear function as a model function. There are 4 reasons why it is used.
There are many methods to study linear phenomena because linear function is easy. If linear approximation can be used, various methods can be used to study.
Linear function is easy to understand. So it leads us to use data-analysis to study the world.
We often get good output using normal-distribution even if the distribution is not like the shape of the normal-distribution because it is the robust theory. Linear-approximation is also robust theory.
Even if the plot is not like the shape of the line, linear-approximation outputs some good knowledge if the plot has tendencies of increase or decrease.
For example, it is used as the first method to divide the variables in cause-and-effect analysis.
Mathematics has the idea to make functions. The function is the sum of functions. And it is approximated from easier function. One of them is Taylor expansion.
By the idea, it is said that "Linear function is enough for the very small range."
There are many cases that daily situation or experimental ideal situation are in the "very small range". Classical science has found the phenomena as "laws".
Non-linearity is normal phenomena in the nature. Linearity is the phenomena like "line". But non-linearity is not only for a curve. Curves are a part of non-linearity. Chaos is one of the examples of non-linearity.
There are not many methods for non-linearity generally. But the method for lines is applied for curves.
Even if linear-approximation is powerful, it often does not go well for real data.
In my experience, it is the limit of mathematical approach. Other approaches help to go over the difficulty. For example, "Graphical approach", "Study the background of the data and the phenomena" and so on,
NEXT 
Partial Correlation
