独立成分分析（Independent Component Analysis ： ICA）は、 主成分分析 や 因子分析 と似た手法ですが、これらよりも新しいです。
会場内に、話し手が散らばっていて、マイクは話し手の位置とは関係なく散らばっている時、 それぞれのマイクが集める音声データには、複数の話し手の声が混ざり、 その混ざり具合がマイクの位置で変わって来る状態になります。
こうした音声データを、個々の話し手だけの音声データに分解する問題は、 「カクテルパーティ問題」と呼ばれます。
独立成分分析は、カクテルパーティ問題の解法として紹介されるのが一般的です。
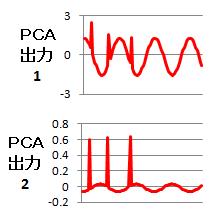
独立成分分析の例として、「正解1」、「正解2」のデータが混ぜ合わさって、
「入力1」、「入力2」のデータになっている場合をやってみました。。
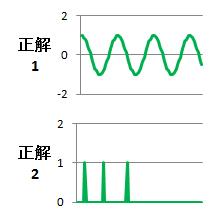
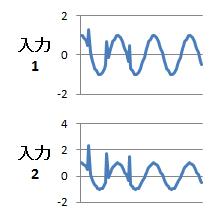
出力は下図のようになり、ソフトは正解のデータを知らなくても、正解のデータに近いものが出て来ました。
（「出力1」の方は、プラスとマイナスが逆ですが）
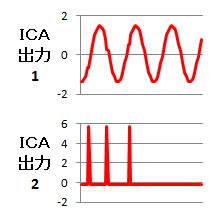
出力2のグラフで、値が高くなっている部分は、
入力1や入力2のグラフで、波形が乱れているように見えているところです。
乱れているように見えていますが、入力1の場合は、波形の最大値と最小値の範囲よりも、飛び出るほどではありません。
入力2のデータを、ヒストグラムにすると下図になります。
乱れている部分は、全体的な分布からは外れていますが、分布の裾の中に入っているようにも見えます。
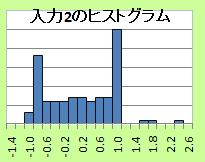
こういった部分をうまく分離してくれるので、独立成分分析は面白いです。
独立成分分析は、 外れ値 や 異常値 を機械的に分けてしまう（フィルタリングする）方法として紹介される事もあります。
主成分分析 には、たくさんの変数を、少ない変数に要約する使い道がありますが、 独立成分分析も、これと同じ使い道ができます。
主成分分析で抽出される要約された変数には、「それぞれに相関がない」、 「データ全体への寄与率の大きいものから、優先して抽出される」、 「正規分布が仮定されている」という性質があります。 一方、独立成分分析は、独立していることを評価する尺度を用意して、要約された変数を探しますので、 この性質がありません。
上記の例題を、主成分分析（PCA）で実施した結果が、下図になります。
正解に近い形に、きれいに分離しませんでした。
出力1については、元の形がほとんど残っていて、入力1と入力2の平均のようになっています。
なお、このページの事例は、独立成分分析の方が、解析したいデータや、解析の目的に合うケースです。 どちらを使っても、大差ない事もあります。
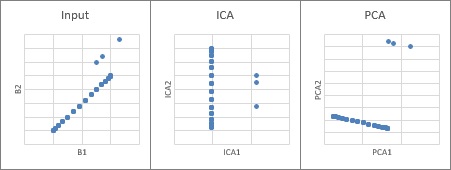
独立成分分析が、データに対してどのような処理をしているのかは、上の波形データを散布図にするとわかります。 左の図が入力データ、中央が独立成分分析の結果、右が 主成分分析 の結果です。
独立成分分析では、外れている３つの点の特徴がひとつの軸だけでわかるようにデータが回転していることがわかります。
主成分分析は、この図を見る限りでは、何とも言えない回転をしているように見えます。
因子分析 は、「いくつかの因子があって、その影響の度合いで、データの中にある各変数の値が決まっている」、という考え方をしますので、 この点は独立成分分析と同じです。 （このため、このサイトでは、因子分析の仲間として、独立成分分析を分類しています。）
独立成分分析は、もともとカクテルパーティ問題が意識されているせいかもしれませんが、特徴のある信号を抽出するような時は、うまく独立成分が分かれるようです。 一方、際立つようなところがないような因子が元になっていとると、うまく分かれないです。
因子分析は、独立成分分析でうまく分けられたないような時に、うまく分けられることがあります。 この性質は、 Rによる隠れ変数の分析 で利用しています。
因子分析 では、変数の数が少ないと、因子に分解する計算ができないことがあります。
独立成分分析と 主成分分析 との共通点として、計算をできるかどうかという点で、変数の数の影響は受けないことがあります。
音声データは、データに時刻の情報が入っています。 また、音声データに限らず、時刻の情報が入っていて、しかも時刻が重要な事は、よくあります。 「何月何日」や「何時何分」のようなデータはなかったとしても、データの順番が時刻の順を表している事もあります。
このようなデータを、きれいに分離するには、時刻の情報は貴重な情報源になります。
しかし、 主成分分析 や 因子分析 には、この時刻の情報を考慮する理論にはなっていません。 ちなみに、この特徴は、 多変量解析 や データマイニング といわれる手法では、一般的な特徴です。
独立成分分析も基本的な部分では、この時刻を考慮する理論になっていません。 ただ、もともとがカクテルパーティ問題を解く事を目標としているためと思いますが、 時刻の情報を分析の中に取り込むための方法は、いろいろと検討が進められて来ています。 この検討は、他の手法を使う時にも参考になります。
ちなみに、上記の例題では、データの順番（時刻の情報）は考慮されていません。 考慮しなくても、けっこううまく分類するのが、独立成分分析のすごさのようです。
Rによる実施例としては、 Rによる隠れ変数の分析 のページがあります。
「入門 独立成分分析」 村田昇 著 東京電機大学出版局 2004
体系立ててシンプルにまとまっています。
音声データを独立成分分析する時は、前処理として、短時間毎に区切って
フーリエ変換
した周波数のデータを作り、そのデータに対して独立成分分析をします。
「詳解 独立成分分析 信号解析の新しい世界」 Aapo Hyvarinen・Juha Karhunen・Erkki Oja 著 東京電機大学出版局 2005
時系列の情報を入れる話など、話題が豊富です。
独立成分分析のモデルには、データの持っている時系列の情報が入っていません。
そこで何らかのフィルターを通して時系列の情報が入るように前処理したデータに対して、独立成分分析をします。
フィルターの簡単な例として、移動平均が紹介されています。
また、
自己相関
を使う方法もあります。
「独立成分分析 多変量データ解析の新しい方法」 甘利俊一・村田昇 編著 サイエンス社 2002
大学のゼミを舞台にした、台本のような形で書かれています。
上記の「入門」と「詳細」の間くらいの内容でした。
独立成分分析は、カクテルパーティ問題を例に出される事が多いですが、
実用上の例として、脳波の分析の話にかなりのページが割かれています。
時間相関（自己相関）を仮定できると、比較的簡単な計算で、独立成分分析ができるようになるそうです。
画像を基底関数の和で表現し、基底関数の係数は、できるだけ多くが0になるように選ぶのが、スパースコーティング。
音は、進むと減衰するが、減衰の度合いは、周波数毎に違う。
そのため、受信側は、周波数毎に減衰の度合いの違う信号になる。
これは時空間混合信号と呼ばれる。
元の信号に、一種のフィルターをかけた信号と考える事もできる。
逆フィルターは、イコライザーと呼ばれる。
また、元の信号を復元する事は、デコンボリューションと呼ばれる。
順路
次は
項目反応理論
