微分データと積分データ のページは、データの物理的な意味を考えて使う話が中心でした。 微分については、「差分（引き算）」という簡単な計算でも、解析でわかる事を広げる事ができます。 このページは、その使い方の話です。
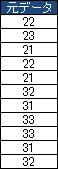
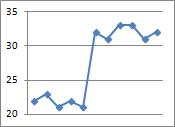
例えば、下のような表のデータとグラフがあるとします。 データの順番は、時刻の順になっていて、時間間隔は等間隔とします。
値の低い時が続いた後に、高い時が続いている事がわかります。 結構、急な変化があります。
異常状態の工程解析
のように、品質の分野のデータ解析では、高いか、低いかよりも、変化したタイミングが重要な事がよくあります。
このデータが 多変量解析 のひとつの変数として使われる時には、「値の低い時と、高い時がある」という情報は解析の中で使われます。
ところが、「急な変化が１回ある。その時以外は、変化は小さい。」という情報は使われません。
時間的な変化の情報が解析で使われないのは、多変量解析全般の特徴です。 「たくさん変数があるから、多変量解析が役に立つかも」、と思っても、この弱点が絡むような解析は、うまく行きません。
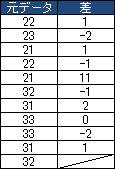
下の表は、次の値との差の値を追加しています。 このページでは、このようなデータを「差分データ」と呼ぶことにしました。
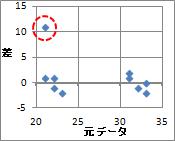
図は、元の値を横軸、差分データを縦軸にした散布図です。
差分データが高い時のある事、つまり、急な変化のある事が、この図でもわかります。
ちなみに、前のデータとの差を分析する方法は、 管理図 の中の「X-R管理図」という方法でも使わています。
コンピュータの中では、無限小が扱えないため、 微分をして速度を求める時は、差分が一番粗い近似計算になります。 そのため、差分データは、微分データですし、時間で微分しているので速度データです。
ちなみに、速度（微分した量）を散布図の縦軸にする解析は、 微分方程式 の性質を調べる方法として知られています。
差分データを 多変量解析 のデータに加えると、変化の大きさも多変量解析で解析できるようになります。
また、変化の向きは、元の値と組み合わせると、細かな状況が解析できるようになります。 例えば、「温度が異常に高い」という状況になっているとしても、さらに高くなりつつあるのか、低くなり始めているのかによって、 対応は変わって来ますが、このような事が、わかるようになります。
差分データを加えると、 多変量解析の大きな弱点のひとつが解消されます。 また、 １次データの解析 が豊かになってきます。
上記では、「次の値との差」を差分データにしました。 この他には、「前の値との差」も、差分データとして使えます。
差の計算（引き算）は、 データの時間間隔が等間隔の時には、定性的なことを知る解析なら問題なく使えます。
等間隔でない時や、速度の単位を定量的に把握したい場合は、差の値を時間間隔で割って、 時速や、秒速のような単位で計算する事もできます。
時間間隔を使う計算の応用として、「前後の値も入れた3点の傾き」なども、差分データとして使えます。 こうなってくると、差分というよりも、速度として正確に求めようとしています。
どの計算が良いのかは、ケースバイケースです。 おおまかには、計算の仕方の結果への影響は大した事はないですが、 変化のタイミングが少しずれて計算されるので、微妙なタイミングが重要な時は、計算の意味を考えると良いです。
「自然現象から学ぶ微分方程式」 森真 著 共立出版 2016
ベクトル場で微分方程式を見る方法や、関数空間、など、微分方程式の見方や扱い方が、一通り解説されています。
１回微分した量を、散布図の縦軸にして、データを見る方法も紹介されています。
「面接触センサからあいまいな「たたく/なでる/震える/押す」を読み取る 研究! 生体センシング×機械学習」 牧野浩二、今仁順也 著 インターフェース CQ出版社 2016
「自己組織化マップ
は、あいまいな情報をあいまいなままで処理するので、人間のあいまいな動作を分類するのにちょうど良い」、と考えています。
8本のセンサについて、触った時から50サンプル分のデータを取り、サンプル間で変化量と最大値を取ると、100次元のデータができます。
このデータについて、「たたく、なでる、震える、押す」を自己組織化マップで分類できるそうです。
つまり、動作の内容をコンピュータに分類して認識させることができるそうです。
この解説は、「ラズパイではじめる人工知能コンピュータ ; 本格人工知能コンピュータへの道」という特集記事のひとつです。
ラズパイ（ラズベリーパイ）という小型のコンピュータに、
人工知能
を汲みこんで、いろいろな事に応用するアイディアが特集されています。
人工知能による、魚の飼育の話などもあります。
順路
次は
数値積分
