近い・遠いだけに注目して２次元に圧縮する方法

距離には、「値が大きいほど遠い」という性質があります。

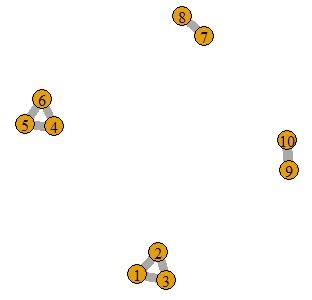
ところで、ネットワーク分析では、「値が大きいほど近い」という性質を持つデータを扱います。例えば、人間の関係が強ければ（大きければ）、関係が近いことがあります。ネットワークグラフは、値が大きい関係のあるものをつないで、グラフを作ります。

このように考えてみると、距離のように「値が大きいほど遠い」という性質のあるデータを、「値が大きいほど近い」という性質に変換すれば、ネットワークグラフで、可視化できるのでは、というアイディアになって来ます。

座標データを再構成する方法との違い

高次元データのネットワーク分析では、距離行列による次元圧縮と違って、座標データの再構成をしません。

そのため、低次元の座標データにすると、矛盾が発生するような場合にも柔軟に対応できます。

ネットワークグラフでは、線（エッジ）で結ばれているかどうかだけが重要です。線を使うことで、高次元データを二次元状に展開することができます。

ただし、線が交差して見にくくなりやすいため、サンプル数が大量の場合には向きません。

「値が大きいほど遠い」を「値が大きいほど近い」に変換する方法は、いくつか考えられます。例えば、
(max - x)
です。値の性質が逆になるだけでなく、値が正の値のままになります。

また、逆数にして
1 / x
でも、大小関係が逆になります。

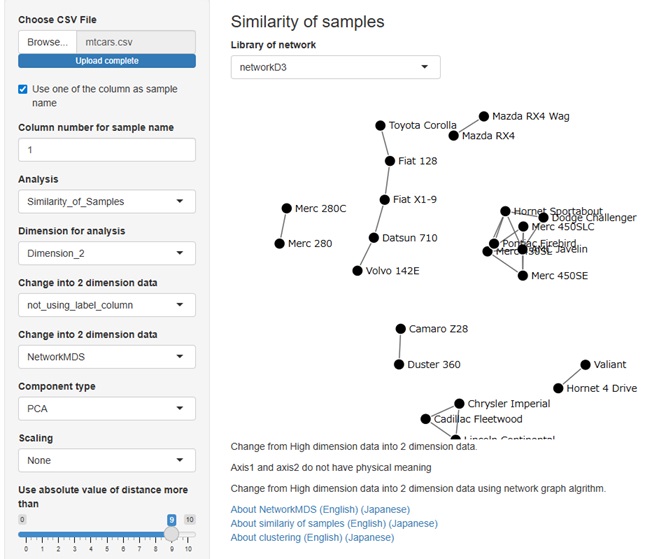
Rによる実施例は、 Rによる高次元データのネットワーク分析のページにあります。
mds

R-EDA1 では、「NetworkMDS」という名前です。
mds