中間層を使った解析

重回帰分析が代表的ですが、一般的な多変量解析では、YとXの直接的な数理モデル（関係式）を調べます。

高度な多変量解析には、XとYの間に中間層となる変数を挟むものがあります。

中間層の使い方や、メリット・デメリットは、データリテラシーとして知っていると良いので、このページにまとめてみました。

中間層を使う解析の強み

XとYを単純な数理モデルで直接結び付ける事が難しい時に、中間層を挟むとうまく行く事があります。

XとYを直接的に結び付ける事ができない理由として、データがそのままでは知りたい情報を表していない事があります。

例えば、ノイズがたくさん入っている場合です。また、データが雑多なために、うまく行かない事があります。

中間層を上手に挟むと、役に立つ情報が強調され、Yとの関係が調べやすくなります。

X、Y、Zの全部を含んだモデルを、ひとつのモデルとして作ります。

ニューラルネットワークの計算方法のひとつに、この方法があります。

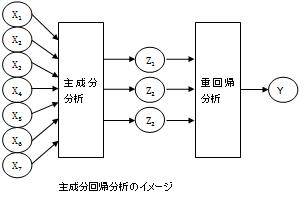
１段階目で、Xを使って中間層のZを作り、２段階目で、ZとYの関係式を作ります。

１段階目で教師なしの学習方法、２段階目で教師ありの学習方法を使います。

代表的なのが、主成分回帰分析です。１段階目で主成分分析、２段階目で重回帰分析をします。主成分がZになります。また、主成分回帰分析と似たものに、主成分MT法があります。

また、複雑なデータ向きの１段階目の手法としては、自己組織化マップやカーネル法があります。自己組織化マップでは、新しく作られた座標の軸がZになります。カーネル法では、Xから新しく作った変数がZになります。

自己組織化マップもそうですが、クラスター分析等の、いわゆる分類のための方法を使う方法もあります。この時は、分類されたカテゴリーをZにすることもできます。（「カテゴリーの数だけ、Zができる」と考えても良いですし、「ダミー変換された変数がカテゴリーの数だけできる」と考えても良いです。）

ディープラーニングは、ちょっと特殊で、教師なしで１段階目をして、参照するモデルを作ってから、教師ありでモデル全体を見直します。

多変量解析や機械学習の方法を使って中間層を作るのは、統計ソフトを使えばできます。しかし、うまく行かない事もあります。

統計ソフトの限界は、統計学から生まれたモデルしか用意されていない点にあります。

また、そのデータがどのようにして集められたのかや、どういうデータなのか、という情報は、扱えないという点もあります。

Xの項目の背景や意味（メタ知識）を把握して、物理学や化学などの式を使って加工すると、中間層がうまく作れる事があります。

因子分析は、古くからある手法のひとつですが、中間層のZを現象の理解に積極的に使おうとします。

心理学関係の文献が多いようです。

社会や経済の仕組みに中間層のアイディアを入れたものに、環境経済学の中間システムの理論があります。

中間層を使うと、良い事ばかりではないです。

Xの特徴を抽出する時に、ノイズだと思っていた中に重要な情報が含まれていると、見落とす事になります。外れ値と欠損値の解析や、異常状態の工程解析でよくあります。

中間層を使った解析よりも、XとYの直接的な関係がわかった方が、その結果を使ったその後の展開が、進めやすい事もあります。

ひとつめの理由が、XとYの直接的な関係の方が、話がシンプルなので、関係者の理解を得られやすいためです。もうひとつの理由は、中間層を挟むと、対策が、XとZ、ZとYの２つについて必要で、それらの連携も考えないといけないためです。