Data <- read.csv("Data.csv", header=T)
library(ggplot2)
ggplot(Data, aes(x=X, y=Y)) + geom_point()
ロジスティック回帰分析 のRによる実施例です。
YとXという変数のあるデータのcsvファイルが、CドライブのRtestというフォルダにあることを想定しています。
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
library(ggplot2)
ggplot(Data, aes(x=X, y=Y)) + geom_point()
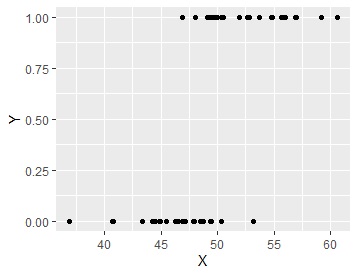
library(nnet)
LR<-multinom(Y ~., data=Data)
probability <- LR$fitted.values
Data2 <- cbind(Data, probability)
library(tidyr)
Data_long <- tidyr::gather(Data2, key="Ys", value = Y, -X)
ggplot(Data_long, aes(x=X,y=Y, colour=Ys)) + geom_point()
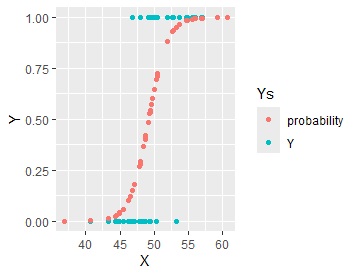
ロジスティック回帰分析では、YとXを直接的に結び付けたモデルを作らないです。 途中を見てみます。
odds <- probability / (1 - probability)# オッズの計算
logit <- log(odds)# ロジットの計算
X <- Data$X
Data3 <- Data
Data3$X <- NULL
Data3 <- cbind(Data3, probability, logit, X)
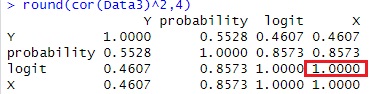
round(cor(Data3)^2,4)# 寄与率（相関係数の２乗）
plot(Data3)
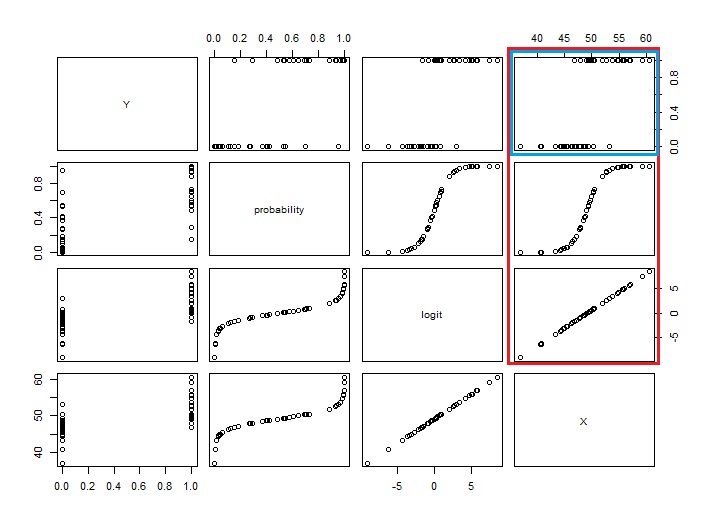
Yが二値なので、YとXの相関は低いです。 しかし、logitとXは完全に相関しています。
ロジスティック回帰分析では、Xと完全に相関して、かつ、その変数を逆ロジット変換して求まる確率が、Yの近似値になるようになっている変数を見つけていることがわかります。
ロジットと確率という２つの変数を仲介することで、YとXの関係性が表現されています。
ちなみに、決定木なら、「Xが50以上は1、Xが50未満は0」といったモデルになります。 ロジスティック回帰分析のモデルは、決定木と違って、明確な境界値がないようなデータの変化を表現できるようになっています。
RA <- lm(Y ~., data=Data)
predictedY <- RA$fitted.values
Data9 <- cbind(Data,predictedY)
library(tidyr)
Data_long <- tidyr::gather(Data9, key="Ys", value = Y, -X)
ggplot(Data_long, aes(x=X,y=Y, colour=Ys)) + geom_point()
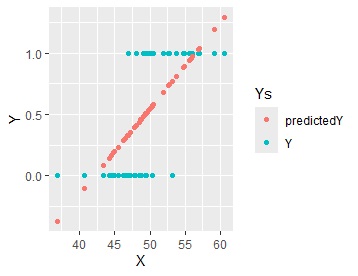
普通の回帰分析をすると、予測値は、0から1の範囲よりも外に出ます。
CRAN
https://cran.r-project.org/web/packages/MASS/MASS.pdf
MASSのマニュアルです。
CRAN
https://cran.r-project.org/web/packages/nnet/nnet.pdf
nnetのマニュアルです。
