ベクトル量子化ロジスティック回帰分析 のRによる実施例です。
ベクトル量子化 で説明変数を１次元の質的変数に圧縮してから、 ダミー変換 で多次元にします。 これを新しい説明変数として、普通のロジスティック回帰分析をします。
一般的なロジスティック回帰分析は、 Rによるロジスティック回帰分析 があります。
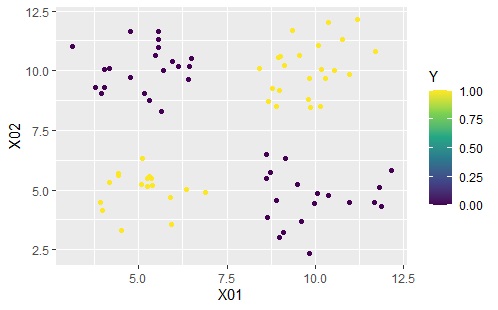
ここでは、以下のデータを使っています。
library(MASS)
library(mclust)
library(ggplot2)
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Y <- Data$Y
Data10 <- Data
Data10$Y <- NULL# Yの列を削除
Data11 <- Data10 # 出力先の行列を作る
for (i in 1:ncol(Data10)) {
Data11[,i] <- (Data10[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))# 正規化
}
mc <- Mclust(Data11,4) # 混合分布法で分類。これは4個のグループ分けの場合
cluster <- mc$classification # 分類結果の抽出
max_output <- max(cluster)
nrow_Data <- nrow(Data11)
dummy_Data <- data.frame(matrix(0, nrow_Data, max_output))
for (i in 1:nrow_Data) {
dummy_Data[i,cluster[i]] <- 1
}
Data5 <-cbind(Data,cluster)# データセットの作成
Data4 <-cbind(Y,dummy_Data)# データセットの作成
gm <- step(glm(Y~., data=Data4, family= binomial(link = "logit")))
predicted_Y <- predict(gm,Data4,type="response")
Data2s2 <- cbind(Data5,predicted_Y)
ggplot(Data2s2, aes(x=X01, y=X02)) + geom_point(aes(colour=predicted_Y)) + scale_color_viridis_c(option = "D")
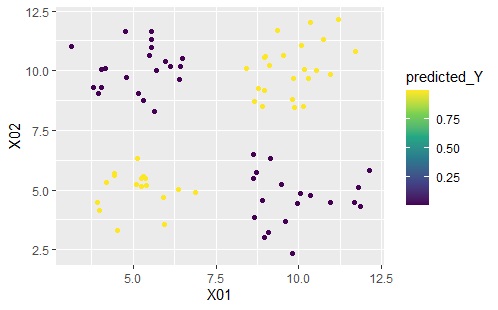
完璧に予測できていることがわかります。
下記で、クラスターがどのように作られたのかが、わかります。
ggplot(Data2s2, aes(x=X01, y=X02)) + geom_point(aes(colour=as.character(cluster)))
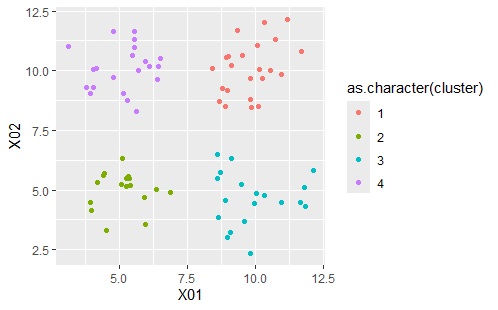
上記は、用意したサンプル全部についてモデルを作って、用意したサンプルと答え合わせをしています。
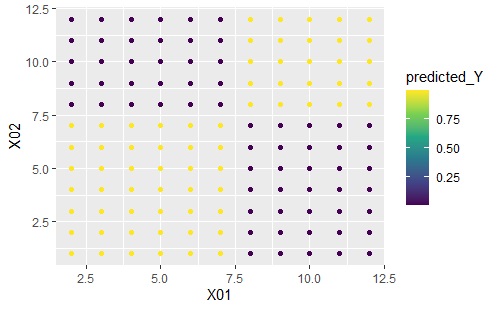
任意の位置について、予測値を求めます。 以下の例は、Data2.csvというファイルに、X01、X02という変数があり、データが書かれている場合です。
Data2 <- read.csv("Data2.csv", header=T) # データを読み込み
Data21 <- Data2
for (i in 1:ncol(Data2)) {
Data21[,i] <- (Data2[,i] - min(Data10[,i]))/(max(Data10[,i]) - min(Data10[,i]))
}
cluster <- predict(mc, Data21)$classification
nrow_Data2 <- nrow(Data2)
dummy_Data2 <- data.frame(matrix(0, nrow_Data2, max_output))
for (i in 1:nrow_Data2) {
dummy_Data2[i,cluster[i]] <- 1
}
Data52 <-cbind(Data2,cluster)# データセットの作成
predicted_Y <- predict(gm,dummy_Data2,type="response")
Data2s22 <- cbind(Data52,predicted_Y)
ggplot(Data2s22, aes(x=X01, y=X02)) + geom_point(aes(colour=predicted_Y)) + scale_color_viridis_c(option = "D")
「機械学習のための特徴量エンジニアリング」 Alice Zheng・Amanda Casari 著 オライリー・ジャパン 2019
名前はついていないのですが、ベクトル量子化回帰分析と同じ内容の方法が、ベクトル量子化の解説の後に、紹介されています。
