クラスター分析による外れ値の検出 では、単にデータを分類するだけでなく、「外れたサンプル」というグループに分類するための クラスター分析 を紹介しています。
サンプルの類似度の分析 のひとつとして、「外れたサンプル」を探索する方法は、 クラスター分析 以外にもあります。
１次元データでは、基本的には、大多数が入る分布がひとつあって、その両端からどのくらい離れているかをみます。
大多数が入る分布が２つ以上ある場合、それらの分布の中間地点で孤立しているサンプルを見つけたい場合は、 箱ひげ図やスミルノフ＝グラブス検定では、見つかりません。 ヒストグラムで見つかることもありますが、見つけにくいです。 この場合は、多次元データの方法を使うと良いです。
１次元分布のグラフ
で見つかります。
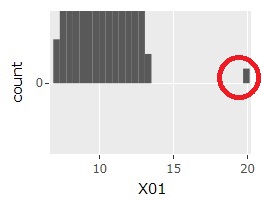
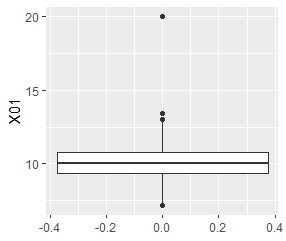
１次元の正規分布を仮定して、分布の一番外側のサンプルが外れ値かどうかを判定します。
多次元データの場合は、どうやって「外れ」を見える形にするのかが方法によって異なります。
高次元を２次元に圧縮して可視化 した時に、孤立しているサンプルは、外れたサンプルです。
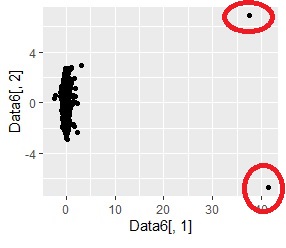
多次元データについて、個々のサンプルが、近くのサンプルからどのくらい離れているのかを調べます。
この結果として、外れ値がどれかもわかります。
One-Class SVM も外れたサンプルの探索に使えますが、「外れたサンプルの探索の方法」ではなく、「多数が所属するグループの境界付近（縁、エッジ）のサンプルをグループ分けする方法」と考えた方が、間違いが少なく、適切な方法になるようです。
外れたサンプルの探索の方法は、どれが外れているかがわからない状態から分析をスタートします。
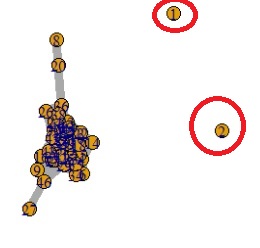
例えば、下図には外れたサンプルが右上に見えていて、 クラスター分析による外れ値の検出 で、外れたサンプル（この場合はグループの番号が「0」）を見つけることができています。
この例では外れたところのサンプルは、４個がグラフではわからないくらい近くに固まっているのですが、 「４個が大多数から外れている」という結果になっています。
４個だとこの結果ですが、４個のある辺りにもっと増えて来ると、それらがひとつのグループに見えて来ますので、「外れ」という結果ではなくなって来ます。
「外れ」と「ひとつのグループ」の境界線の引き方は、手法の種類やパラメタの大きさで変わりますので、一概に言えません。
このため、
外れたサンプルの探索の方法を使った時に、データの状態によっては、思ったように外れたサンプルが検出できないことがあります。
1クラスモデル は、基準とするサンプルのグループを先に決めて、外れているかどうかがわからないサンプルについて、個々に、基準との関係を判定する方法です。
外れているかどうかを判断するところが、外れたサンプルを探索する方法と似ているのですが、１クラスモデルの場合は、 判定したいサンプル同士の関係は扱わないので、判定したいサンプル同士の近さで判定が変わることはないです。
下記は、 Rによる外れたサンプルの探索 のページのコードを使ったものです。
２変数（２次元）のデータについて、データの違いに対して、手法の違いがどのように表れるのかをまとめています。 散布図にした時に、外れ値を、クラスター分析の手法も同じように抽出できるのかを見ます。
DBSCANを使いやすくするために、データは正規化してから分析しています。
結論を先に書くと、以下になります。
グループが１つあって、外れ値は２個あります。
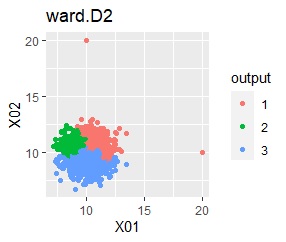
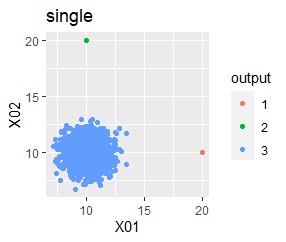
階層型（ward.D2とsingle）では、１つのグループと、外れ値のそれぞれがグループになると仮定して、k=3としています。
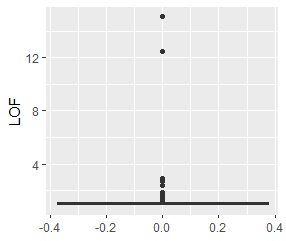
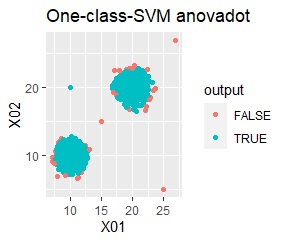
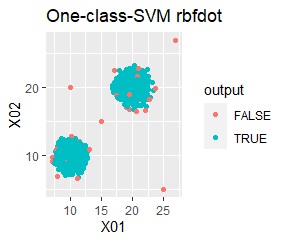
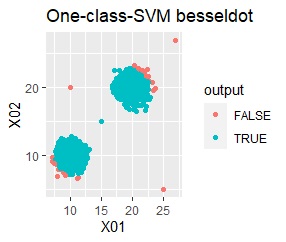
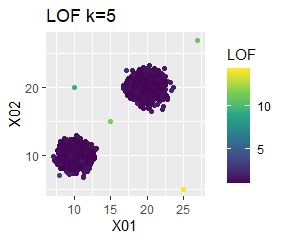
single、DBSCAN、One-class-SVM besseldotは、思ったような分け方をしています。 LOFは、外れたサンプルの値が高いです。 One-class-SVM anovadotも良さそうですがグループの少し内側にも、FALSEと判定されているサンプルがあるので、うまくないかもしれません。
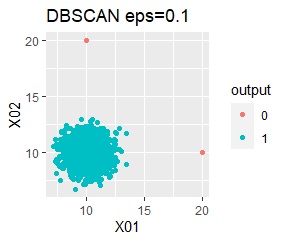
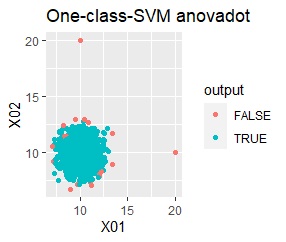
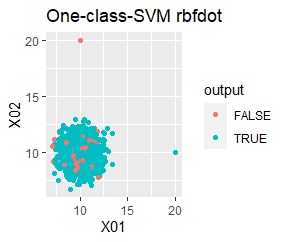
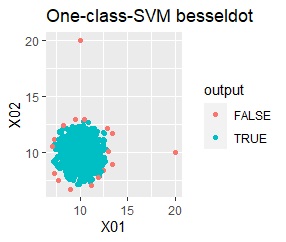
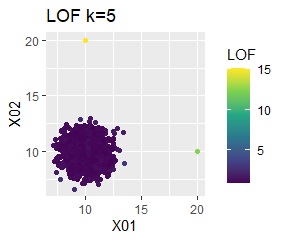
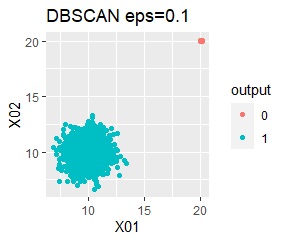
グループが１つあって、外れ値は４個あります。 外れ値の４個は、グラフだと分からないくらい近い位置に固まっています。
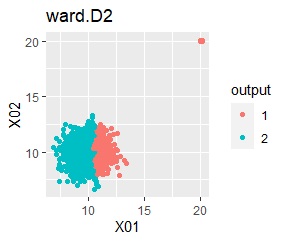
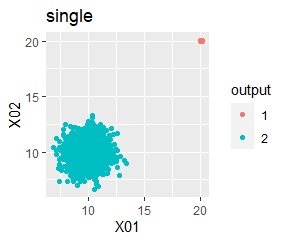
階層型（ward.D2とsingle）では、１つのグループと、外れ値のそれぞれがグループになると仮定して、k=2としています。
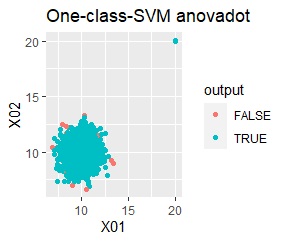
single、DBSCANは、思ったような分け方をしています。 LOFは、外れたサンプルの値が高いです。 One-class-SVM besseldotも良さそうに見えますが、よく見ると外れ値のところに「TRUE」が混ざっています。 ４個中の１個が間違った判定をされました。
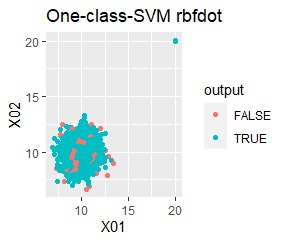
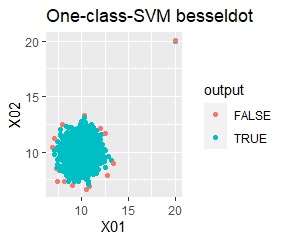
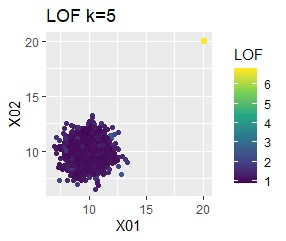
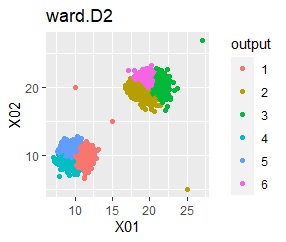
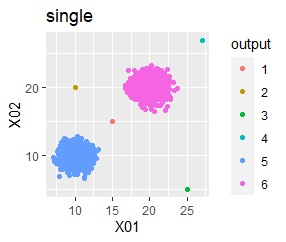
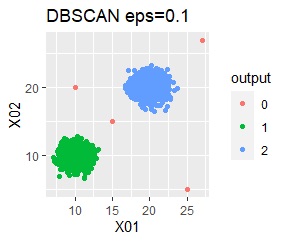
グループが２つあって、外れ値は４個あります。
階層型（ward.D2とsingle）では、１つのグループと、外れ値のそれぞれがグループになると仮定して、k=6としています。
single、DBSCANは、思ったような分け方をしています。
Rによる高次元を２次元に圧縮して可視化 と、 Rによる外れたサンプルの探索 のページがあります。
順路
次は
多対多の分析
