AHPは、「Analytic Hierarchy Process ： 分析的な階層プロセス」の略です。 意思決定論 の文献の中で紹介されている事が多いです。 「階層化意思決定法」とも呼ばれます。
多変量解析 や、 データマイニング の手法は、列が評価項目で、行が各サンプル名になっている表形式のデータを出発点にしていものがほとんどです。 しかし、AHPは、評価項目同士やサンプル同士についての、一対比較のデータを出発点にしています。
学校の試験では、例えば、国語、英語、数学、理科、社会の５科目の総合点で、人を評価します。
５科目の点数を単純に足す方法が、一番簡単です。
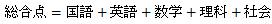
ところで、例えば、「国語、英語、数学の方が、理科、社会よりも重要」と考えて、
「理科と社会の点数は、0.5をかけてから足す」、という計算をする事もあります。
こういう計算は、「重み付けした計算」と言われます。
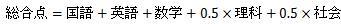
AHPは、重み付けも使った総合点の評価の一種です。 AHPを使っても、最終的に重みをかけて点数を足す部分は一緒です。
こういった評価は、 多基準分析とも呼ばれます。
それぞれの項目の点数のデータがあって、重みのデータが決まっているのなら、 総合点の計算で困ることはないですし、AHPも必要ないです。
AHPは、点数のデータや、重みのデータの取り方からの方法論になっています。
ここでは、コスト、スピード、デザインの３つの項目で評価したいけれども、項目ごとの点数や、重みの大きさが決まっていない例にします。
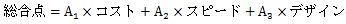
AHPは、プロジェクトの評価方法として使われる事が多いようなのですが、 プロジェクトの案というのは、一般的には、不確定の部分があったり、複雑だったりします。 そのため、重みをいくつにしたら良いのかで悩みますし、 点数をどのように付ければ良いのかでも悩みます。 例の場合でしたら、「デザイン」というのは、どこをどのように点数を付けたら良いのかで、悩むところが多そうです。
しかし、人間は面白いもので、２つの項目だけを取り出して、 「どちらの方が、どのくらい大きいか？」、という判断をするのなら、エイヤッと、できたりするものです。 AHPでは、人間のそういった能力を有効に使います。
どれくらい大きいかは、5段階評価するとします。
例えば、「A1とA2だったら、A1の方がA2より、3大きい。」、
「A1とA3だったら、A1の方がA3より、5大きい。」、
「A2とA3だったら、A2の方がA3より、2大きい。」、
というようにして、評価します。
評価できたら、行列形式の表にまとめます。
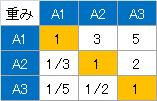
行と列を間違えると、間違った計算になってしまうので、上記の、3、5、2という数字が、行列のどこに入るのかがポイントです。 また、1/3、1/5、1/2という数字も行列に入っていますが、これらの数字は、3、5、2という数字の対角の部分に、逆数として入れられています。
この例の場合でしたら、「A1とA2だったら、A1の方がA2より、3大きい。」、としたので、 「A2とA1だったら、A2の方がA1より、3小さい。」、と書きたいところですが、 大きさの向きが逆の時は、逆数を使うのが、AHPのポイントです。
混乱を避けるために、逆数を使った書き方を、最初の例にしませんでしたが、 仮に、A1とA2を比べた時に、A1の方が小さい、という事になるのでしたら、上記の例で、3を入れていた場所には、1/3が入ります。
次に、この行列の固有ベクトルを求めます。 例の場合は、固有ベクトルが(0.93,0.33,0.17)になります。 これらの値を、重みとして使います。
点数の決定ですが、計算は、重みを決めた時の計算と同じです。 こちらも、5段階評価の場合を例にします。
ここでは、比較したいプロジェクトが、3つあったとします。 例えば、「プロジェクト1」のコストは、「コスト1」と書くことにします。 そして、「コストについて」という事で、プロジェクト同士を比較します。
ここから先は、重みの計算と同じで、行列を作り固有ベクトルを求めれば、固有ベクトルが点数になります。
例の場合は、固有ベクトルが(0.87,0.38,0.33)になります。
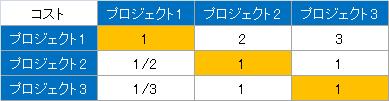
スピードやデザインについても、同じようにして、点数を求めることができます。 このようにして、すべての項目の点数と、重みの値が決まれば、総合点を計算できます。
AHPでは、A1を基準にA2を見る時と、A2を基準にA1を見る時で、数字が逆数になるのは、なんとも不思議です。 また、固有ベクトルを点数や重みとして使うのも不思議です。
一対評価の理論を使うのでしたら、 例えば、A1とA2の関係は、A1/A2を使います。 そして、これをするには、「A1はA2の何倍か？」、という事を推定する必要があります。
しかし、、「何倍くらいですか？」よりも、「どのくらい離れていますか？」の方が、エイヤッは、やりやすいです。 そのため、数学的な正しさは、大目に見ることにして、差を使う理論になっているようです。 差を使いつつも、一対評価の理論も使うので、逆数が登場するようになっているようです。
Rによる実施例は、 Rによる固有値分析 があります。
「AHP事例集 ：階層化意思決定法」 刀根薫・真鍋竜太郎 編 日科技連 1990
最初の10ページくらいで、AHPの手順や特徴がコンパクトにまとまっています。
一対評価を「比」で実施すると、固有ベクトルの計算から、順序のデータが計算できる事が書いてはあるのですが、
「一対比較は差でしているするのに、計算は比の場合でしている」という事について、明確なコメントは見当たりませんでした。
公共事業の選択の話や、
QFD
で出て来る品質展開や機能展開の数値化の話等、様々な分野での事例が集められています。
AHPは、一回計算して終わりではなく、各要素で変化があった場合の影響等、繰り返し計算することが大事。
「入門AHP ：決断と合意形成のテクニック」 木下栄蔵 著 日科技連 2000
評価基準の評価では一対比較を使い、プロジェクト間の評価では絶対評価（横並びの点数付け）を使う方法は、
「絶対評価法」として解説されています。
評価基準同士が独立ではない場合を扱うのが、内部従属法。
評価基準と代替案が独立していない場合を扱うのが外部従属法。そのひとつがANP。
「戦略的意思決定手法AHP」 木下栄蔵・大屋隆生 著 朝倉書店 2007
AHPから始まり、AHPの発展型として、ANP、支配型AHP、集団AHPといったものを解説しています。
各評価基準の重みが、代替案毎に異なっても良いのがANP。
「成功と失敗の科学 ：ゲーム理論からAHPへ」 木下栄蔵 著 徳間書店 2003
損失を最小にしようとするのが
ゲーム理論
で、個人の効用や企業の利潤を最大にしようとするのがAHPとしています。
戦略は目的のことで、戦術は手段のこと。両者を混同してはいけない。戦略が上位。
４章でゲーム理論やAHPは戦略理論とされているのですが、文脈から考えると「戦略をもとに、戦術を選択する理論」でしょうか？
コスト・ベネフィット評価は、コストとベネフィットを散布図にして、図の中での位置から判断を進めます。
そのため、コストとベネフィットという評価項目について、優劣を論じることには意味がありません。
こういう時は、細かな評価項目をコストに関するものと、ベネフィットに関するものに分け、それぞれについてAHPをして、
コストでの総合点と、ベネフィットでの総合点を散布図にします。
「Q&A：入門意思決定論」 木下栄蔵 著 現代数学社 2004
意思決定論
の数理がいろいろ紹介されている中に、AHP、ISM、DEMATELが入っています。
AHPで、絶対評価をする時の方法として、例えば、「良い＝３点、普通＝２点、悪い＝１点」のように、
点数を最初から与えるのではなく、「良いと普通の間の離れ具合は？」というようにして、
点数を一対比較で決めてから、その評価項目を使う方法が紹介されています。
AHPでは、項目間の一対比較を、項目の重みを計算するために使いますが、
ISM（Interpretive Structural Modeling）や、
DEMATEL（Decision Making Trial and Evaluation Laboratory）
では、一対比較を、項目間の階層構造を考察する方法として使います。
ISMは、階層構造の高さを、1と0で表現します。
DEMATELは、関係の程度を、3つ以上の段階で点数付けします。
「システム工学」 中森義輝 著 コロナ社 2002
AHPが「階層化意思決定法」、ISMやDEMATELが「構造モデリング」、
という名前で登場します。
順路
次は
学習する組織
