2番は、X1には無関係に値が決まっているのでX1のP値が大きく、X2のP値が小さくなっています。。
3番は、交互作用が強い場合で、交互作用項X1:X2のP値が小さくなっています。この場合が、２つの変数の相関が強い場合です。
4番は、交互作用がまったくない場合で、X1とX2のP値は小さく、交互作用項のP値は大きくなっています。
1
,
2
,
3
,
4
,
機械学習 には、手法の分類する時に、 教師ありと教師なしの学習 という２つに分けることがあります。
対数線形分析は、この分け方だと「教師なし」になるのですが、実行する時には、 一般化線形モデル という、「教師あり」の方法を計算の中に含むことになります。 こういった点もあり、対数線形分析は特殊な手法ですが、この特徴があるので、他の手法ではできない分析ができます。
実験データの解析 を知っているのなら、 対数線形分析は、 回帰分析 のように理解するよりも、 分散分析 として理解する方が、わかりやすいように思っています。 いわゆる分散分析との違いは、頻度（計数値、カウントデータ）に当てはまりを良くするために、ポアソン回帰分析を使う点です。
ロジスティック回帰分析 は、計算の中で対数を使う 回帰分析 です。 筆者は、対数線形分析を初めて聞いた時に、名前から、「 ロジスティック回帰分析 と同じか、似たようなもの」と思ったのですが、この理解は間違いでした。 たしかに対数も回帰分析も使いますが、使い方が違います。
下記に対数線形分析の２つの使い道がありますが、この２つの使い道という点では、対数線形分析は、 独立性の検定 と仲間になります。 独立性の検定 との違いは、３つ以上の変数の分析でもスマートにできるところになります。
対数線形分析の使い道は、大きく２つに分かれます。 分割表 のデータのモデル化の使い方としての使い方と、 変数の類似度の分析 になります。
分割表 のデータは、棒グラフにしたりして、分析することが多いと思います。
分割表の値の決まり方の背後に数式があれば、対数線形分析でこの数式を導ける場合があります。
相関係数を使って、 多変量データの相関分析 をする方法は、量的変数だけのデータに使いますが、 質的変数だけの時の方法として、対数線形分析が使えます。
変数の類似度の分析として使う時は、 質的変数が並んでいるデータセットを 分割表 のデータセットに集計する作業が前処理になります。
対数線形分析では、質的変数が複数ある場合でも、分割表の場合でも、分析のスタートのデータとして使えます。
対数線形分析では、いずれの場合も、下記のような形式に変換して、処理します。
対数線形分析の学問的に正確な定義と数式について、筆者はよくわかっていないのですが、 ネットで見る限りでは、頻度の数字が縦一列に並んでいる分割表に対して、 ポアソン回帰分析 を使う方法が紹介されていることが一般的なようです。 そのため、このページでも、筆者の作ったソフトでも、この方法を対数線形分析（Log linear model）としています。
分割表で、頻度の数字が並んでいる列が目的変数になり、それ以外の列が説明変数になります。 説明変数は質的変数ですが、 ダミー変換 して量的変数に変換することで、一般化線形モデルが使えるようになります。
また、一般的な 重回帰分析 は、各変数の線形和を使う１次モデルが使われることが多いですが、 対数線形分析では、交互作用を見るため、各変数の積の項も含む二次モデルを使います。 「交互作用項が有意になる変数の組み合わせが、相関の高い変数の組み合わせ」と考えて、 変数の組み合わせを調べます。
交互作用項が有意にならない場合は、変数の組合せの効果は、数値の大きさに関係していないことになります。 単独の変数の効果だけか、変数のカテゴリとは関係なく数値の大きさが決まっている、という意味になってきます。
冒頭の話に戻ると、このような方法を使うため、「教師なし」なのに、「教師あり」の方法を使っています。
対数線形分析は、入力データがどのようなもので、結果がどのようになって来るのかがイメージしにくいので、例を作ってみました。
まず、1番ですが、値に差があまりない場合は、どの変数もP値が大きいです。
2番は、X1には無関係に値が決まっているのでX1のP値が大きく、X2のP値が小さくなっています。。
3番は、交互作用が強い場合で、交互作用項X1:X2のP値が小さくなっています。この場合が、２つの変数の相関が強い場合です。
4番は、交互作用がまったくない場合で、X1とX2のP値は小さく、交互作用項のP値は大きくなっています。
1,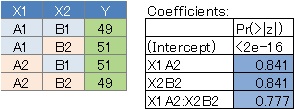
2,
3,
4,
質的変数が３つある場合です。
飽和モデルを仮定したので、すべての変数の組み合わせが評価されましたが、P値が大きい変数がかなりあります。
この場合は、「相関が高い変数の組み合わせはない」、と言えます。
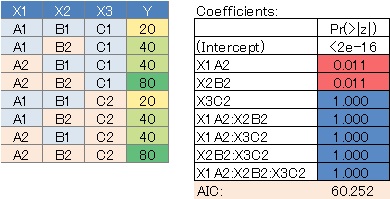
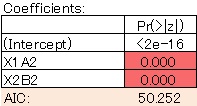
モデルがすっきりしました。AICも小さくなったので、この方が良いモデルと言えます。
Rの実施例は、 Rによる対数線形分析 と、 Rによるクロス集計表の回帰分析 のページがあります。 スタートになるデータの形式が異なります。
R-EDA1 では、 行と列に項目名が配置されている 分割表 データのモデル化と、 変数の類似度の分析 の２つの使い道が、両方ともできるようになっています。
分割表のデータのモデル化は、
「Two_way_GLM」で、
「poisson_log」を選ぶとできます。
ちなみに、「gaussian_identity」を選ぶと、頻度のデータではない場合のモデル化で、数量化Ⅰ類になります。
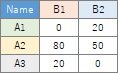
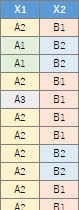
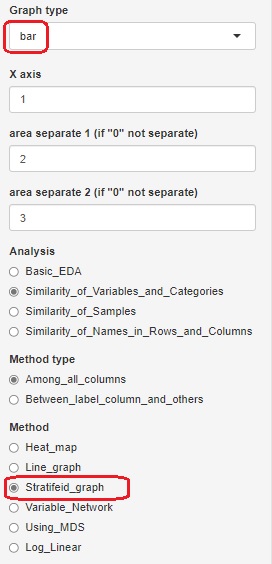
分割表に集計されていない質的変数のデータを使う場合は、やり方が２つあります。 「Method」で「Log＿Linear」を選ぶと、データセットの全部の変数をスタートにして、モデルの探索が始まります。 「Stratifeid_graph」を選んで、「Graph type」を「bar」にすると、グラフの作成に選んだ変数をスタートにして、モデルの探索が始まります。
この機能の場合、量的変数が混ざっていると、
量的変数は
１次元クラスタリング
をして質的変数として扱われます。
また、この例は、２変数ですが、３変数以上でもできます。
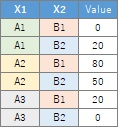
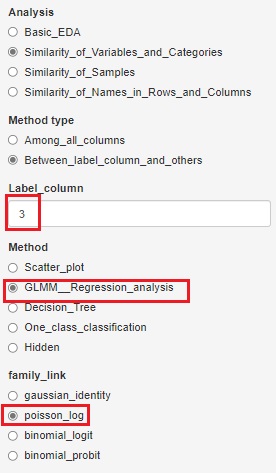
縦一列に数値が入っている分割表からスタートする場合は、一般化線形混合モデル（GLMM）の機能を選ぶとできます。
例の場合は、３列目に数値が入っているので、「３」を指定する必要があります。
この形の分割表になっていると、３変数以上でもできます。
「質的情報の多変量解析」 松田紀之 著 朝倉書店 1988
対数線形モデルの本です。
１次元から始まり、最後は潜在クラス分析になっています。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
数量化Ⅲ類
では、複数の質的変数の絡みが考慮できないとして、それが考慮できる方法として対数線形モデルを挙げています。
そして、質的変数の
グラフィカルモデリング
の理論にしています。
「分割表の統計解析 二元表から多元表まで」 宮川雅巳・青木敏 著 朝倉書店 2018
同著者の上記の本から、さらに多元分割表からの相関分析の方法を研究した内容になっています。
同志社大学 金明哲先生のページ
Rと対応分析
https://www1.doshisha.ac.jp/~mjin/R/49/49.html
順路
次は
連関係数
