クロス集計表の回帰分析 の、Rによる実施例です。
データの性質によって、 対数線形分析 を使う場合と、 数量化Ⅰ類 を使う場合があります。 いずれも、 重回帰分析 の応用です。
表の値は、頻度や関係の強さを表していて、大きいほど関係が強い場合です。
０が一番小さな値で、「関係なし」の意味になっているとします。
下記のデータの場合は、BとTが一番強い関係を表しているとします。
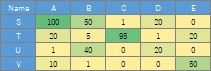
対数線形分析 を使います。
データの変換の部分以外は、 Rによる質的変数の対数線形分析 と同じです。
コードの例では、一番左の列はサンプル名として使われます。
library(tidyr) # ライブラリの読み込み
library(MASS) # ライブラリの読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- tidyr::gather(Data, key="Name2", value = Val, -Name) # 縦型に変換（Nameの列以外を積み上げる）
summary(step(glm(Val~.^2, data=Data1,family=poisson))) # 対数線形分析
この例だと、「(Name + Name2)^2」がモデル式の右辺として最終的に残っているので、
行と列の項目の単純な足し合わせ以外の要因で、値が決まっていることがわかります。
データによっては、例えば「Name2」が最後に残ることがあります。
この場合は、行の項目とは関係なく、値が決まっていることになります。
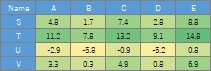
表のデータは、その条件の時の値を表します。
数量化Ⅰ類 を使って、数値と項目の関係を数式で表す方法です。
library(tidyr) # ライブラリの読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- tidyr::gather(Data, key="Name2", value = Val, -Name) # 縦型に変換（Nameの列以外を積み上げる）
summary(step(lm(Val~., data=Data1))) # 数量化Ⅰ類
決定係数（R-squared）が0.9991なので、非常に高いモデル式ができていることがわかります。
結果の見方ですが、「TとB」の組み合わせの推論の値は、
5.010 + 6.120 -3.100 = 8.03
ということになります。
多重共線性
の回避のために、AとSがダミー変数から抜けていますが、例えば、
「AとT」の組み合わせの値は、
5.010 + 6.120 = 11.13
と求めます。
なお、結果として、有意なモデル式が作られた場合は、複雑な規則で値が決まっていることは推察できますが、 どのような規則なのかはわかりません。
