ポアソン分布の例が上図です。
ポアソン回帰分析は、 一般化線形モデル の一種です。 残差が、ポアソン分布になっている回帰分析です。
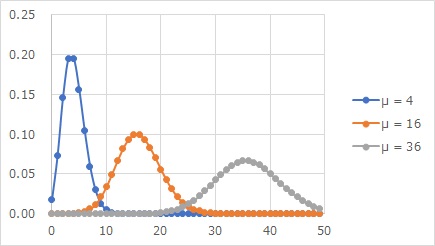
ポアソン分布の例が上図です。
ポアソン分布は、０以上の整数しかないです。 まれにしか起きない現象を数えた時のデータの分布として知られています。
ポアソン分布の特徴として、平均値と分散が同じ値になる点があります。 標準偏差は、平均値の平方根になります。 このため、上図のμというのはそれぞれの分布の平均値なのですが、μが大きいとばらつきが大きいことがわかります。 平均値が、4、16、36なら、標準偏差は、2、4、6です。
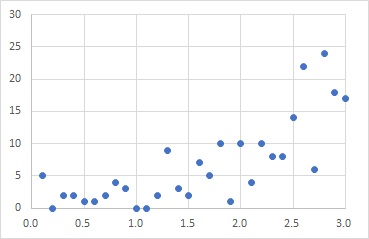
ポアソン回帰分析にぴったりの分布が上のようなものです。
Xが大きくなると、ばらつきが大きくなっています。
一般化線形モデルでポアソン回帰分析をする時は、ポアソン分布を選ぶだけではなく、リンク関数に対数を選ぶのがデフォルトです。 つまり、ポアソン回帰分析では、Xに対して、Yの平均的な値は、指数的に増えることも考慮する場合が一般的になっています。 上の例の場合も、直線ではなく、指数関数的と考えた方が良さそうです。
これは、自然界の現象で、「増える」という時は、直線的ではなく、指数関数的に増えることが多いという特徴から来ているようです。
ポアソン回帰分析には、Xが増えるほどばらつきが大きくなるモデルとしてだけではなく、指数関数的に増えるモデルとしても意味があります。
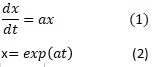
モデル式(1)は、xの増加率が、その時のxの値のa倍で比例することを表しています。
(1)に当てはまるxとtの関係式が(2)で、指数関数になっています。グラフは例えば、下のようになります。
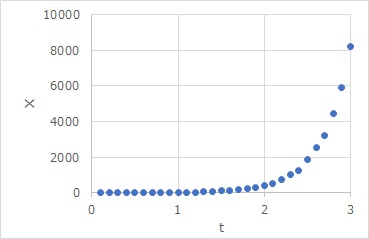
このように比例というメカニズムが背後にあった時に、目に見えているものが指数関数になっていることがあります。
ポアソン回帰モデルで、リンク関数を恒等関数（Y=AX+B）にした場合と、 比例分散の回帰分析 は、似たようなモデルになります。
いずれもXが大きければ大きいほど、Yのばらつきが大きくなります。
違いはまず、モデルの形の違いで、ポアソン回帰モデルでは、「Xが大きくなると、ばらつきが大きくなる」という特徴が、ポアソン分布の中に入っています。 これに対して、比例分散モデルでは、元にする分布のばらつきは固定で、Xをかけることで、「Xが大きくなると、ばらつきが大きくなる」を扱っています。
ポアソン分布は、計数値（０以上の整数）の分布です。比例分散モデルは、計数データや、正である事に限定されないです。
ポアソン分布は、平均値の平方根がばらつきの大きさになります。 平均値というのは、あるXの時の平均的な値です。
比例分散モデルは、Xに比例して、ばらつきが大きくなります。平方根ではないのも違いです。
ポアソン分布は、ある程度平均値が大きくなると正規分布として近似できます。
比例分散で分布の形を正規分布と仮定した場合、平均値が小さい時は、ポアソン回帰と比例分散モデルは、残差の分布の形が違いますが、 平均値が大きい時は、いずれも正規分布の形になります。 上記のようにポアソン回帰だと、「平方根」になるので、正規分布という点は共通でばらつきの大きさだけが違いになって来ます。
ポアソン回帰分析のソフトについては、 一般化線形混合モデル のページにあります。
「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 久保拓弥 著 岩波書店 2012
植物の研究では、ポアソン回帰が必要というところから始まっています。
「空間統計学 ：自然科学から人文・社会科学まで」 瀬谷創・堤盛人 著 朝倉書店 2014
空間統計学ではポアソン回帰が多い。
順路
次は
正規化による有向相関分析
