単回帰分析
のページで図解していますが、回帰分析では、「残差が等分散」、「残差が正規分布」、「直線で近似」、「線形和（加法）」の４点を前提としたモデルが基本になっています。
これがぴったり当てはまるのは、下図のようなデータです。
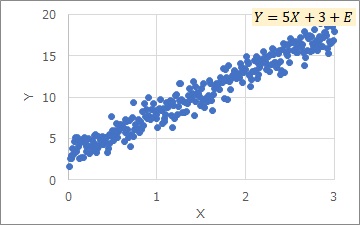
これらの前提に当てはまらない場合の方法も、世の中にはあります。例えば、以下です。
一般化線形モデルは、「残差が等分散」、「残差が正規分布」、「直線で近似」の３つの前提を、一般化した理論です。 ただし、「非等分散、非正規分布、非直線は、何でもOK」という理論ではないので、 比例分散の回帰分析、曲線の回帰分析、乗法モデルがいらなくなる、という話ではないです。
Y = AX+B を Y=g(AX+B) として、g()を任意の関数とすることで、曲線に対応できるようにしています。
g()の逆関数がf()です。 f(Y) = AX+B は、リンク関数と呼ばれています。
リンク関数は、「正規分布の時は、恒等関数」、「ポアソン分布の時は、対数」といったように、世の中でよくある組合せがデフォルトになっています。
一般化線形モデルは、正規分布以外の任意の分布も、残差の分布として仮定します。
ソフトでは、選択できるようになっています。
ポアソン分布を仮定した場合は、ポアソン回帰分析と呼ばれます。 二項分布を仮定した場合は、 ロジスティック回帰分析 と同じです。
等分散以外への対応は、正規分布以外の対応と連携しています。
例えば、ポアソン分布は、分散の大きさが平均値の平方根です。 回帰式は、それぞれのXでの平均値の値を示す式なので、分散の大きさも、それぞれのXで変わります。 Xが大きくなると、平均値が大きくなるモデルなら、Xが大きくなると、分散も大きくなります。これによって、等分散ではなくなります。
一般化線形混合モデル は、一般化線形モデルをさらに拡張したモデルになっています。
Rによる変数の選択 と Rによる一般化線形混合モデル のページにあります。
「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 久保拓弥 著 岩波書店 2012
ポアソン回帰の必要性から、一般化線形モデルに広がっています。
「空間統計学 ：自然科学から人文・社会科学まで」 瀬谷創・堤盛人 著 朝倉書店 2014
付録で、一般化線形モデルを簡単に解説しています。
順路
次は
ポアソン回帰分析
