は、傾きがAで切片がBの直線を表す式です。
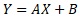
は、傾きがAで切片がBの直線を表す式です。
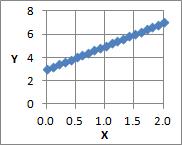
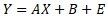
は、回帰分析のモデルです。
Eというのは、誤差（Error）で、この部分があることで、ばらつきながら直線に近い形でデータが並んでいることを表現します。このサイトでは、
ばらつきモデル
と呼んでいます。
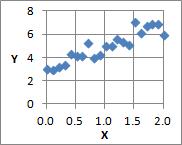
上の式は、「加法（足し算）モデル」の一種です。 加法モデルほど、有名ではないですが、誤差を含む乗法（掛け算）モデルというものもあります。 このページは、誤差を含む乗法モデルの話です。
誤差を含む乗法モデルについての、世の中の解説は、大きく分けると２種類あります。 誤差項の形が違っています。
このページで、「乗法モデルexp(E)」と呼ぶのは、下記のような式です。
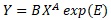
こちらは、「multiplicative model」で検索すると出て来ます。
加法モデルと乗法モデル のページにあるように、加法モデルを変形させると、この式になります。
このページで、「乗法モデルE」と呼ぶのは、下記のような式です。
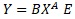
乗法モデルEは、時系列解析のモデルとして紹介されることが多いです。 また、「乗法モデル」で検索して出て来る解説は、筆者の見た範囲では、全部、乗法モデルEでした。
乗法としては、素直な形になっています。
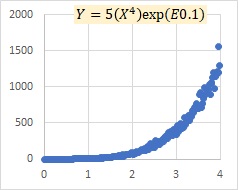
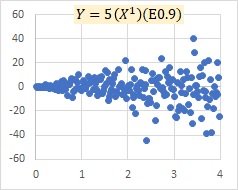
グラフの中の「E0.1」というのは、かっこの中の数字が、平均値が0、標準偏差が0.1の正規分布の乱数であることを表します。
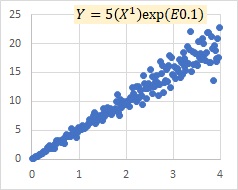
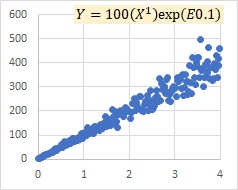
乗法モデルexp(E)の例です。
Xが大きくなるにつれて、Yのばらつきが大きくなってくることを表すモデルなのは、乗法モデルEと似ていますが、Yが全体的に大きくなることも表しています。
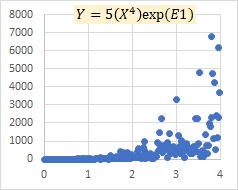
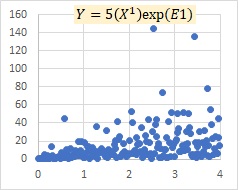
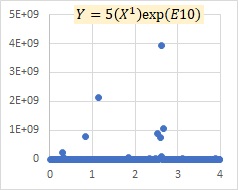
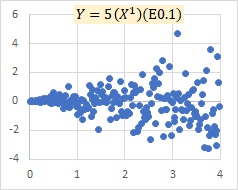
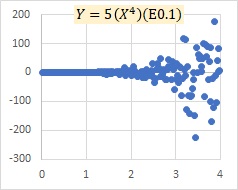
乗法モデルEの例です。
Xが大きくなるにつれて、Yのばらつきが、プラスとマイナスの両方で、大きくなってくることを表すモデルになっています。
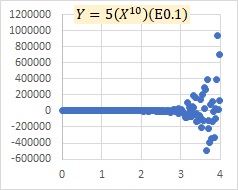
上記のグラフでは、周期性はありません。 周期性を扱うなら、 ARモデルとその発展形 のようにして、加法モデルで扱うと簡単です。
「乗法モデル」で調べると 時系列解析 の方法として紹介されている記事が、たくさん見つかります。
Xを時系列と考えると、乗法モデルは、「時間が経つほど、不確定要素の影響が増大していく」ということを表すモデルになります。
加法モデルと乗法モデルは、見た目がだいぶ違いますが、変換できる関係があります。 加法モデルと乗法モデル のページにまとめています。
乗法モデルと比例分散モデル は、似ていますが、使い道がだいぶ違います。
上記で、２種類の乗法モデルの例を書いていますが、そこでは、「平均値が０」としています。 回帰分析では、回帰直線の上下のばらつきがあり、回帰直線はそのばらつきの平均値を表しています。 Eに対して、「平均値が０になるようにばらつく」とするのは、自然な考え方と思います。
ところで、「誤差はこういう性質だから、・・・」と考え始めると、「平均値は０」という話になるのですが、 現実にどんなものであるかにこだわらず、乗法モデルの式の形だけで考えるのなら、０以外も式としては作れます。
このサイトでは、平均値が０の場合を「狭義」、それ以外を「広義」と呼ぶことにしています。
広義の場合は、様々な形が考えられますが、「例えば、平均値が５の正規分布」を仮定すると、 その乗法モデルは、加法モデルのような性質があります。 こういった性質は 加法モデル的乗法モデル のページにまとめました。
狭義の乗法モデルでは、ばらつきの効果を「E」という部分に入れています。 このモデルでは、「何だかわからないけれども、ばらつきがあって、ばらつきの大きさがEで表せる」といった発想で、「E」が入っています。
広義の乗法モデルでは、Eは、ばらつくような性質を持った何かです。 Yは、そのような何かに他の要素を掛け合わさったものと考えます。
乗法モデルについて、このページでは、式の形から、狭義と広義、というように分けていますが、そこに含むことができる物理的な意味は、「狭い・広い」といった違いではないです。
DeepSquareのページ
https://deepsquare.jp/2021/03/time-series-predict-model/
時系列データの予測モデルとして解説しています。
BellCurve 統計WEBのページ
https://bellcurve.jp/statistics/course/23739.html
時系列データの予測モデルとして解説しています。
ScienceDirectのページ
https://www.sciencedirect.com/topics/mathematics/multiplicative-model
とても丁寧にまとまっています。
順路
次は
加法モデルと乗法モデル
