加法モデル的乗法モデル

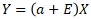
proportional regression
という比例分散モデルの、「a+E」の部分は、「平均値がaになっているばらつき」という解釈ができます。そのように考えると、aとEは２つで１つのものを表しています。比例分散モデルは、「a+E」とXが掛け合わさっている乗法モデル（広義の乗法モデル）です。

比例分散モデルは、加法モデル的乗法モデル

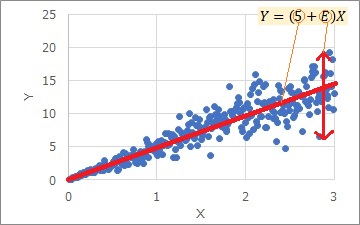
proportional regression
上のグラフは、比例分散モデルの例です。

比例分散モデルの、aの部分は傾き、Eの部分はY軸方向のばらつきの大きさを決める数字になっています。

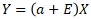
proportional regression
という式で比例分散モデルは表現できますが、

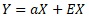
と書いて、aXとEXの２つの効果が合わさっているモデルと解釈すると、対策も分けて考えられるようになるので、便利です。

このように乗法モデルとして表現できるけれども、加法モデルのように書くことができ、加法モデルのように解釈できるモデルを、「加法モデル的乗法モデル」とここでは呼んでいます。

偶然誤差と系統誤差のうち、偶然誤差は、平均値が０の分布で、系統誤差は、平均値のずれになっています。

「a+E」の部分を、「平均値がaになっているばらつき」と考えるという事は、「偶然誤差と系統誤差の両方を入れた」という解釈ができます。

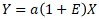
proportional regression
という形で書けば、比例比例分散モデルも、乗法モデルになります。

ただ、「1」というのは、乗法モデルの形にするために便宜的に使われているものなので、特に物理的な意味がないです。この点が、比例分散モデルとは違います。そのため、モデル式としては、不自然な感じがします。