比例比例分散モデル

「比例比例分散モデル」は、筆者の造語です。「比例比例」と書いているのは、誤植ではなく、二重に比例する所から来ています。

比例分散と似ていますが、ちょっと違います。ばらつきがEとXの積になってくるのが、比例分散ですが、比例比例分散では、傾きaがさらにかけ合わさります。
SN ratio

比例分散が１個の時は、元のEがわかっている場合でもない限り、比例分散モデルと比例比例分散モデルは区別ができないです。比例分散の線形混合モデルのように、比例分散が複数ある場合に、それらの複数の関係性が比例比例分散モデルで説明できる可能性があります。

比例比例分散モデルの例

下のグラフのA、B、C、Dでは、Eの大きさは同じで、傾きだけ違います。 Eの大きさは同じなのですが、傾きがかけ合わさるので、傾きが大きいほど、見た目のばらつきも大きくなっています。
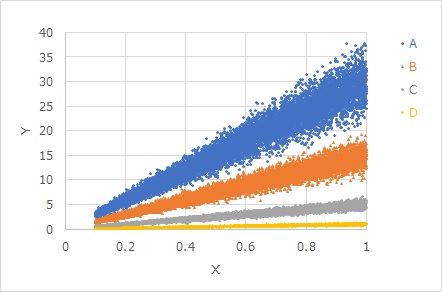
SN ratio

比例比例分散モデルは、傾きaと、ばらつきの大きさEだけで決まっています。それぞれは、下記の式で求まります。
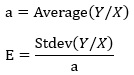
SN ratio

aは、Y/Xという変数を作って、それの平均値を計算すると求まります。また、Eは、Y/Xという変数の標準偏差を計算してから、それをaで割ると求まります。

この求め方は、比例分散の回帰分析の応用です。

「２つ以上の比例分散があった時に、これらは、比例比例分散モデルの関係になっているのではないか？」と調べたかったとします。

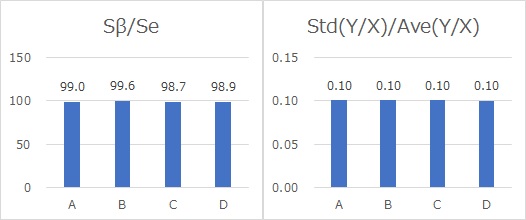
動特性のSN比のページにあるように、 Sβ/Seや、Ste(Y/X)/Ave(Y/X)という尺度を使うと、「Eは同じはず」という仮説を調べることができます。これらの尺度で、ほぼ同じ値になれば、「Eは同じ」と考えられます。

上のグラフの場合を計算すると、下のようになります。 Eが共通で、比例比例分散モデルが当てはまることが確認できます。
SN ratio

比例比例分散モデルに対して、「こんなモデルに当てはまるデータは、現実にはないのでは？」と思う人は多いかもしれません。

確かに、比例比例分散モデルになっているデータは、一般的なデータサイエンスでは出て来ませんが、品質工学では、数十年前から一般的に知られています。

上記のように比例比例分散モデルを評価する尺度が、品質工学から提案されています。

品質工学では、動特性のSN比を使ってデータを評価することは、昔から研究されているのですが、モデル式を導出するような方向では研究がないようです。

このページでは、比例比例分散モデルとして、
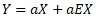
proportional regression
という式を紹介していますが、筆者が考えたものです。難しいものではないので、先行した研究があってもおかしくないですが、筆者の知る限りではないようです。

モデル式ができると、予測とシミュレーションもできるようになって来ます。

このページの冒頭の書き方は、加法モデルのような書き方で比例比例分散モデルを書いています。

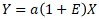
proportional regression
と考えて、
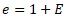　(例えば、平均値１の正規分布)
と考えれば、

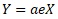
となるので、乗法モデルと言えます。

加法モデルと乗法モデルのページに両者の相互変換がありますが、それとは違う変換をしています。 Eは残差のばらつきなので、「平均値が０の分布」というのがイメージしやすいですが、「平均値が０」以外でも良いのなら、乗法モデルになります。

なお、数学的には比例比例分散モデルが乗法モデルで表現できても、実務上では、比例比例分散モデルは、加法モデルの形で考えた方が良いと思います。加法モデルの形だと、グラフの中で、傾きとして見える部分と、ばらつきとして見える部分を分解して考察できるためです。