「一般化比例分散モデル」は、筆者の造語です。 比例比例分散モデル を一般化したものですが、 一般化線形モデル の特殊なものでもあります。
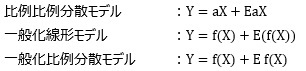
比例分散が１個の時は、元のEがわかっている場合でもない限り、比例分散モデルと比例比例分散モデルは区別ができないです。 比例分散の線形混合モデル のように、比例分散が複数ある場合に、それらの複数の関係性が比例比例分散モデルで説明できる可能性があります。
比例比例分散モデル の一般化というのは、比例分散のaXの部分を、Xの関数なら何でもOKにした点です。
一般化線形モデル の特殊なもの、というのは、一般化線形モデルでは、誤差の部分が、Xの逆リンク関数f(X)の何らかの関数になっている点です。
一般化比例分散モデルでは、Eになっている分布が、f(X)に比例する場合だけを想定しています。 これと似ているのが、 ポアソン回帰分析 です。 ポアソン回帰分析 では、Eとしてポアソン分布を仮定していますが、ポアソン分布の標準偏差は、f(X)の平方根になっています。
品質工学 では、 標準SN比 という評価指標がありますが、 標準SN比 で測ろうとしている非線形のデータが、ちょうど一般化比例分散モデルが当てはまるものになっています。
下のグラフでは、Y方向のばらつきが、Yの大きい時に大きくなる様子がわかります。
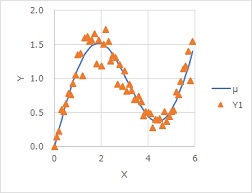
品質工学
では、非線形のデータの分析方法として、標準状態を横軸にしたグラフに変換することを提案しています。
上のグラフで、この変換をすると下になります。
標準状態は、各Xの平均値μを置いています。
μは、Y=f(X)の部分です。
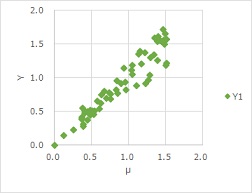
この変換をすると、データが直線的に並び、 比例分散の回帰分析 として進められるようになります。 品質工学では、これを 標準SN比 で評価します。
順路
次は
リッジ回帰分析
