標準SN比

標準SN比は、名前に「標準」とついているので、「標準的なSN比」と誤解されやすいようです。また、 SN比の中では、比較的、後になって考えられたものなので、「従来のSN比よりも素晴らしいSN比」と誤解されやすいようです。

実際は、どちらでもないです。標準SN比は、標準状態のロバスト性の評価や、非線形の動特性の評価に使えるSN比です。

標準状態のロバスト性評価

標準状態というのは、標準（基準）と考えている（決めている）状態のことです。例えば、基準になる装置が出す値です。また、決められた条件で動いている工程で、突発的に起きる外乱があるなら、外乱がない場合が標準状態です。

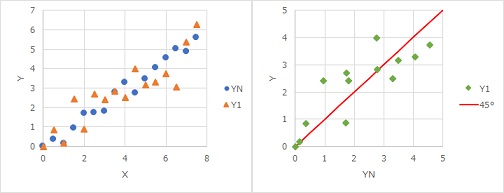
Normal SN ratio
例えば、上の左の図のようなデータになります。YNが標準状態で、Y1が条件を変えた場合です。

ロバスト設計としては標準状態と変わらないことを目指しますので、この変化を評価する必要があります。

この評価が上の右の図です。横軸を標準状態のYN、縦軸をY1とします。すると、Xのことを気にせずに、Yの違いだけを評価できるようになります。図には「45°」という線がありますが、YNとY1がまったく同じなら、この線の上に点が並びます。この線からの離れ具合が、データのばらつき方を表しています。

標準状態は、文字通り標準になる状態があれば、それになります。

標準状態がなかったとしても、２個以上の条件のデータがあるのなら、それらの平均を標準状態と置く方法もあります。この場合は、平均的な状態からのばらつきを見る方法になります。
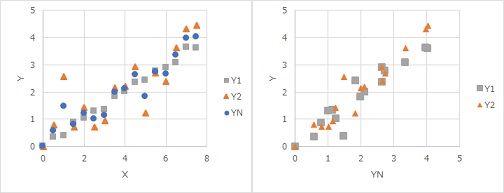
Normal SN ratio

上の図は、Y1とY2の平均値がYNになっています。条件が２個の場合です。左図では、Y1の方が、直線からのばらつきが大きいように見えますが、右図ではY1もY2も同じような感じになっています。これは、平均を取っているのが原因になります。

平均値を標準状態とする方法は、条件が２個だとあまり利点がなく、３個以上ある時に条件の違いを見る方法としては利点があるようです。下の例は、４個の場合です。 Y1、Y2、Y4に比べて、Y4のばらつき方が大きい様子が、右図からもわかります。
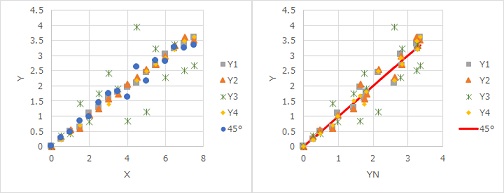
Normal SN ratio

標準状態のロバスト性評価は、擬似相関の応用技にあるように、相関係数でも評価できます。実験データの分析の時に使う尺度として、品質工学からは標準SN比が提案されています。

特性とSN比の関係に動特性のSN比がありますが、標準SN比は、Xの代わりに、標準状態のYを使います。

この使い方は、擬似相関の応用技と同じです。

動特性の実験の、さらなるデータ解析としても、標準状態の解析の考え方が使えます。第２段階の解析と言っても良いかもしれません。

まず、普通に動特性の実験を解析して、ベストな条件を出します。そして、ベストな条件を標準状態とみなします。すると、ベストな条件と他の条件の比較に、標準状態の解析が使えます。

動特性と非線形現象にあるように、動特性のSN比だと、XとYの非線形の関係があった時に評価できません。

ところで、標準状態のロバスト性評価では、標準状態のYと、別の条件のYの関係を見ます。この時、Xとの関係がどうなっているのかは影響しなくなるので、XとYが非線形の関係だとしても、標準状態のロバスト性評価はできるようになっています。つまり、標準SN比は、非線形の動特性の評価をする方法になります。

例えば、下の左の図では、XとYが非線形の関係になっています。標準状態YNとY1だけの関係が右図になります。データが直線的に並んでいるので、相関係数や標準SN比で標準状態からのばらつき方が評価できることがわかります。
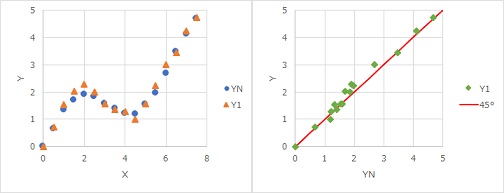
Normal SN ratio

非線形でデータ直線的に並ぶもうひとつの例は、以下のような場合です。
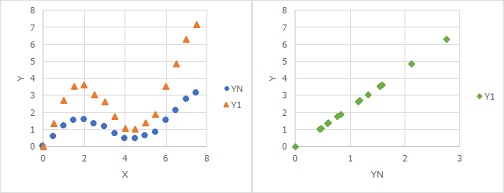
Normal SN ratio

Yに比例して、ばらつき方が大きくなる場合は、データが直線的に並びます。

XとYが非線形の関係でも良い、というのは、Xが量的データの時だけでなく、質的データの時にも当てはまります。

「標準SN比は、非線形の動特性の評価をする方法になります。」と書きましたが、XとYの関係を調べていないです。

「非線形の関係」はいろいろあるので、非線形の関係に使う場合は、ケースバイケースの対応が必要になります。「グラフを見ながら適切な水準を取る」、等の対応です。

条件の違いによるYの違いは見ていますが、その時にXがどうなっているのかは見ていないので、場合によってはXとの関係を確認する必要があります。

標準SN比は便利ですが、「標準状態との関係を見る」や「非線形の評価ができる」という部分だけで理解すると、誤用につながりやすいようです。

下記のように、標準状態との違いが、ばらつき方だけなのかが、ポイントになります。このポイントは、データの数字や、SN比を見てもわからないので、グラフで確認すると良いです。

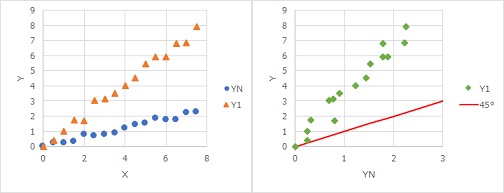
Normal SN ratio
まず、上の左図のような場合は、右図のように45°の線とは違うところでばらつきます。標準状態とY1の違いは、ばらつき方だけではないです。

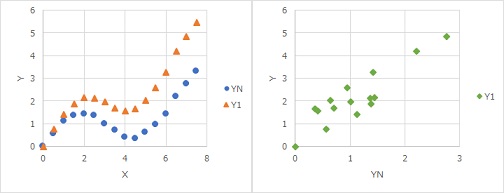
Normal SN ratio
標準SN比で、非線形の評価ができないのが、上図のような場合です。 Xに比例して、ばらつき方が大きくなっている場合は、データが直線的に並びません。

そのため、標準SN比による評価が妥当とは言えなくなります。

品質工学では、標準SN比で評価しようとしているデータが、どのような式でできているのかの研究はないようです。一般化比例分散モデルは、そのような式として、筆者が考えたものです。

「ベーシック 品質工学へのとびら」　田口玄一・横山巽子共著　日本規格協会 2007
田口氏による解説です。

「基礎から学ぶ品質工学」小野元久　編著　日本規格協会　2013
標準状態として、誤差因子の２水準の実験データの平均値を使う方法を紹介しています。