比例分散というのは、上のような分布です。 Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。 これの統計学的なアプローチは、 比例分散 や 比例分散の回帰分析 にあります。
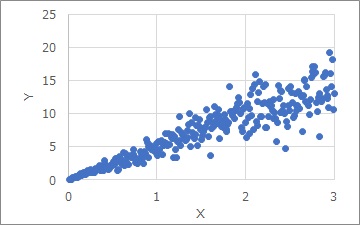
比例分散というのは、上のような分布です。
Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。
これの統計学的なアプローチは、
比例分散
や
比例分散の回帰分析
にあります。
品質の分野では比例分散は、よく出て来ます。 品質工学 でも比例分散の分析方法があります。 特性の分類 としては、望目特性と動特性の２つのアプローチがあります。
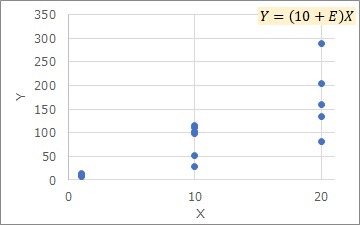
望目特性として扱う時は、比例分散の横軸の値は使いません。
横軸の値が一定なグループを「水準」と考えて、水準毎にSN比を計算します。
望目特性のSN比は、データのばらつきを平均値の大きさで割ります。 例えば、上記のように比例分散そのもののような時は、見た目のばらつきは違っていても、SN比としては「同等」として評価されます。
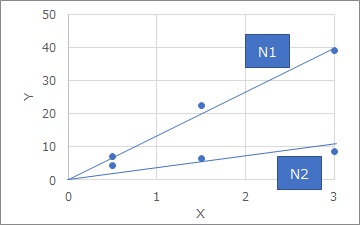
動特性の誤差因子で扱う場合は、例えば、上の図のように、誤差因子N1、N2のそれぞれの時でYとXの関係を調べます。
動特性の誤差因子を使う時は、誤差因子によって傾きが異なるという、傾きのばらつきで、比例分散のような様子を扱っています。
Xが大きければ大きいほどY方向のばらつきが大きくなる性質を、誤差因子で評価しようとした時に、上のグラフのようになるとは限らないです。
上のグラフでは、N1とN2のそれぞれ単独については、データがほぼ一直線に並ぶことを想定しています。 「Xが大きければ大きいほどY方向のばらつきが大きくなる」という性質そのものになっている誤差因子があるのなら、こうなることもあります。 例えば、外気温によって、装置の寸法がわずかに変わっている事が、ばらつきの原因になっている場合です。
しかし、誤差因子と考えられるものがあったとしても、それが傾きに影響しているものになっているとは限りません。
上記の２つの方法は、いずれも比例分散にアプローチしているものの、この分布をシステムとして扱うような方法にはなっていません。
動特性のSN比 は、もともと比例分散をイメージして作られた理論ではないようですが、 動特性のSN比 にあるように、比例分散の評価に使えます。
下記の参考文献では、乗法型（ 乗法モデル ）を提案しています。
比例分散の回帰分析
のページにある内容を品質工学でよく使われるSN比と感度という表現にするのなら、
比例分散のSN比と感度は、以下のものが良いように筆者は考えています。
Y/Xの分散（標準偏差）や平均値は、比例分散の形を直接的に表すものなので、比例分散の評価としては、
他の
動特性のSN比
よりも便利です。
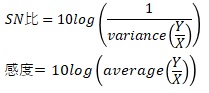
品質工学では、「X」は「M」と書くことが多いです。varianceは分散で、averageは平均です。 品質工学では、「分散」や「平均」という言葉を使わずに、その計算式を直接出すことが多いです。
「乗法型計測システムにおけるパラメータ設計 応答関数モデリングとパフォーマンス測度モデリングによる最適化」 河村敏彦・ 元山斉 著 日本品質管理学会 品質 42(2) 2012
信号因子Xと誤差因子Nが入ったモデルとして、
Y = β(X,N) M ε
という式が提案されています。
εは、平均μ、変動係数cの逆ガウス分布としています。
この論文は、このモデルに合うSN比の提案や、信号因子と誤差因子の交互作用の検討がされています。
筆者の調べた範囲では、傾きβと残差項εの掛け算を考えているモデルは、品質工学では他にありません。
この論文では、「こういうグラフになっているデータだから、こういうモデル」という説明はないのですが、
比例比例分散モデルと、似た考え方で作られた式のようです。
順路
次は
エネルギー比型・変動比型のSN比
