トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

動特性のSN比

特性の分類 のページで、動特性の８つの種類について説明しています。 このページは、それぞれの動特性について、それを測るのに適したSN比を説明します。 ただし、残念ながら、全部ではないです。

なお、このような動特性の説明は 品質工学 の文献では出て来ないです。 筆者が調べてみたところ、このような形が一番良いと思ってまとめましたが、不備があれば、直す方針です。

動特性の種類と、適切なSN比の対応

• 等分散特性１ ： -log(Ve)　：Veは誤差分散。残差（Y-βX）の不偏分散
• 等分散特性２・等分散特性４ ： log(R2／(1-R2)) ：R2は決定係数・寄与率と呼ばれる。相関係数の２乗、βXの積和／Yの２乗和で計算
• 等分散特性２ ： log(β2/Ve) ： 「動特性のSN比」と一般的に呼ばれているものの簡易版。β2とは、傾きβの２乗
• 等分散特性２ ： log((Sβ-Ve)/r/Ve) ： 「動特性のSN比」と一般的に呼ばれているもの。SβはβXの積和。rは、Xの２乗和
• 比例分散特性１ ： -log(Std(Y/X)) ： Std(Y/X)は、Y/Xの標準偏差。分散でも良い
• 比例分散特性２ ： log(Sβ/Se) ： エネルギー比型・変動比型のSN比のひとつ。Seは、誤差平方和。残差の２乗和
• 比例分散特性２ ： -log(Std(Y/X)/Ave(Y/X)) ： Ave(Y/X)は、Y/Xの平均値
• 等分散特性３・比例分散特性３・比例分散特性４ ： 適切なSN比はなし。原点が基準になるように変換してから、等分散特性１、比例分散特性１、比例分散特性２にする。

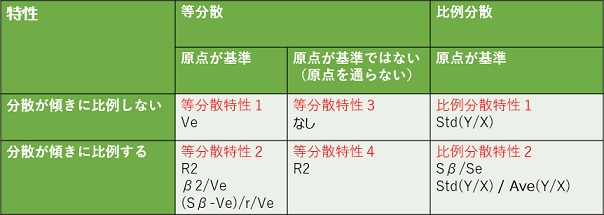
品質工学のSN比 は、
「ばらつきが小さい　＝　SN比が大きい」
、ということが計算されるように作られた尺度です。 logの前に「-」があるものは、「ばらつきが小さい　＝　数字が大きい」という尺度になっています。

R2は、0から1までの比率データなので、SN比として使う場合は、 オッズ（オメガ変換）した方が良いです。

一般的な統計学や、従来の品質工学との関係

動特性のようなデータを扱うのは、一般的な統計学では、 回帰分析 になります。

回帰分析 では、ばらつきの大きさを残差で判断したり、RやR2を使って判断します。 等分散を想定するのが普通ですし、「分散が傾きに比例する」といったことを考えることはないです。

上記の分類では、一般的な統計学では想定しないことや、従来の品質工学が踏み込み始めていた領域について、方法論を整理した形になっています。

動特性ごとに適切なSN比を調べる方法

静特性のSN比 については、特性と、それに相応しいSN比の関係が、いろいろな文献で紹介されています。 一方、動特性については、こういった分類は世の中にないようです。（筆者の知る限りですが）

「比例分散の場合に、変動比型が合っている」と言った説明のある文献が１冊あるのですが、上記のような分類まで踏み込んだものはないようです。

そこで、筆者が調べた結果が、上記の対応関係になります。

下記は調べた方法です。 それぞれの特性について、４つのグループのデータを用意しました。 ４つのグループで同じ値になるのなら、その特性としては同じということを、定量化できることになります。

なお、比例分散特性３・４については、実務で出会うことがとても考えにくく、出会ったとしても、データをずらして、比例分散特性１・２にすれば良いので、調べませんでした。

等分散特性１の評価に適したSN比の探索

等分散は、比例等分散と違って、傾きが異なっていても、ばらつきが同じです。

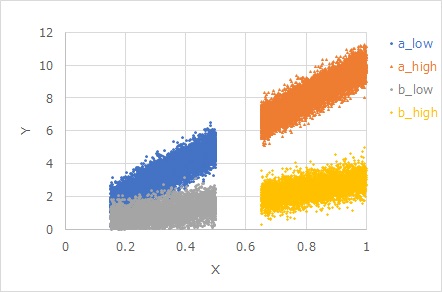
下図は
Y = β X + E
という式で作られたデータです。 aとbは、Eが共通でβだけが違います。また、Xの領域も２種類用意しています。そのため、４つのグループになっています。 βが違っても、見た目のばらつきは同じです。

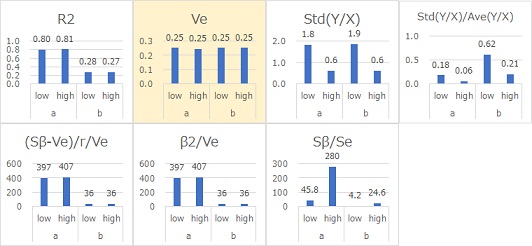
SN比が同じ値になったのは、Veです。 VeがSN比として適していることがわかりました。

なお、 Veは、等分散がどの程度の大きさなのかを、直接的に表す尺度です。

等分散特性２の評価に適したSN比の探索

下図は
Y = β X + β E
という式で作られたデータです。 aとbは、Eが共通でβだけが違います。 Eが共通でも、βがかけ合わさることで、βが大きいほど、見た目のばらつきも大きくなっています。

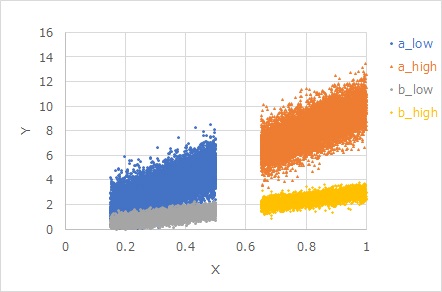
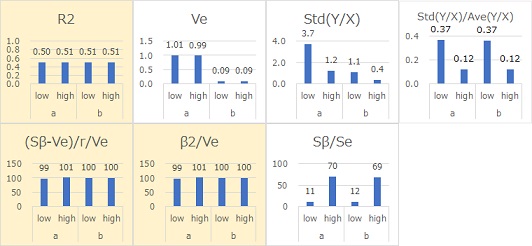
Veは、直線からのYの距離（残差）を表します。Yaで0.99、Ybで約0.09というのは、標準偏差がそれらの平方根の1と0.3なことがわかります。 等分散の場合は、Veがばらつきを直接的に表しています。

R2、(Sβ-Ve)/r/Ve、β2/Ve、Sβ/Seは、SN比がほぼ同じ値になっています。 R2、(Sβ-Ve)/r/Ve、β2/Ve、Sβ/SeがSN比として適していることがわかりました。

等分散特性３の評価に適したSN比の探索

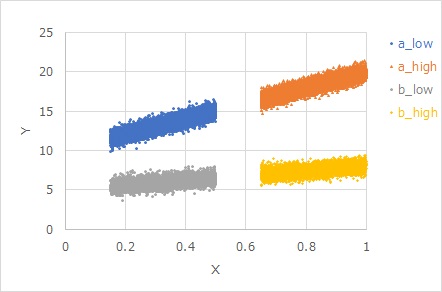
下図は
Y = β X + E X + c
という式で作られたデータです。

等分散特性３の評価に適したSN比は、この中にはありませんでした。

等分散特性４の評価に適したSN比の探索

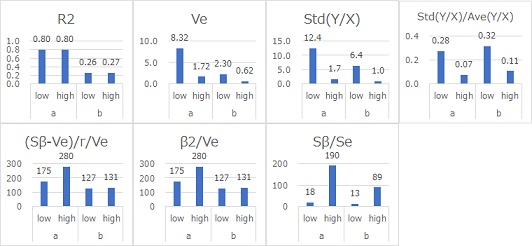
下図は
Y = β (X + E)
という式で作られたデータです。

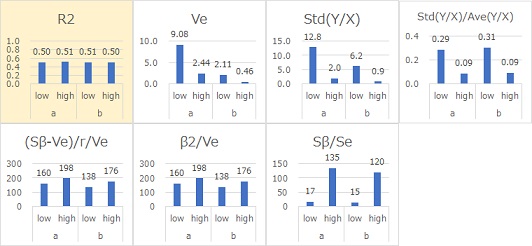
R2は、SN比がほぼ同じ値になっています。 R2がSN比として適していることがわかりました。

比例分散特性１の評価に適したSN比の探索

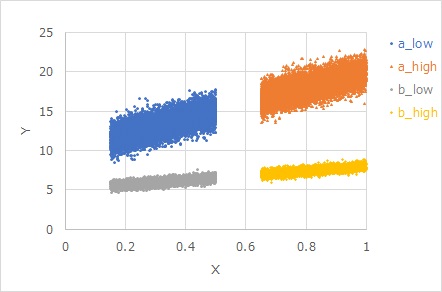
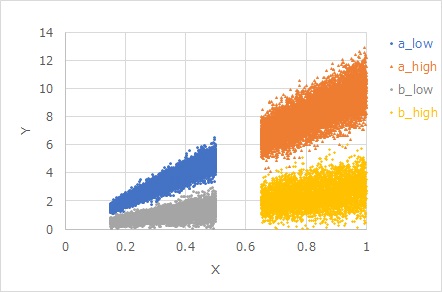
下図は
Y = β X + E X
という式で作られたデータです。比例分散になっています。 aとbは、Eが共通でβだけが違います。βが違っても、同じXでは、見た目のばらつきは同じです。 Xが大きいほど、見た目のばらつきが大きくなっています。

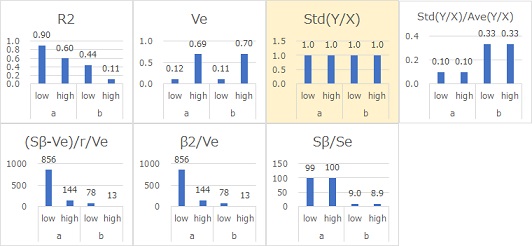
Std(Y/X)は、SN比がほぼ同じ値になっています。 Std(Y/X)がSN比として適していることがわかりました。

なお、Std(Y/X)は、比例分散の形を直接決めるものなので、この値が、ばらつきの大きさを直接的に表しています。

比例分散特性２の評価に適したSN比の探索

「比例比例分散モデル」というのは、筆者の造語です。 同じXの時のばらつきが、Xの値と、傾きβの値の両方に比例します。

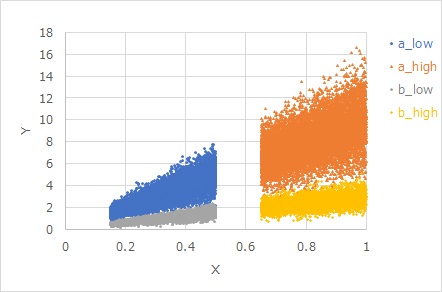
下図は
Y = β X + β E X
という式で作られたデータです。比例比例分散モデルになっています。 aとbは、Eが共通でβだけが違います。 Eが共通でも、βがかけ合わさることで、βが大きいほど、見た目のばらつきも大きくなっています。 また、Xが大きいほど、見た目のばらつきが大きくなっています。

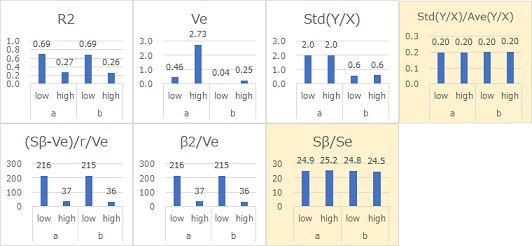
Sβ/Seと、Ste(Y/X)/Ave(Y/X)は、SN比がほぼ同じ値になっています。 Sβ/Seや、Std(Y/X)/Ave(Y/X)がSN比として適していることがわかりました。

なお、Std(Y/X)/Ave(Y/X)は、比例比例分散の形を直接決めるものなので、この値が、ばらつきの大きさを直接的に表しています。

等分散と比例分散

参考文献

「基礎から学ぶ品質工学」 小野元久　編著　日本規格協会　2013
変動比型のSN比が紹介されています。
従来の動特性のSN比は、比例分散のような場合に対応していない点を指摘しています。 さらに変動比型は、分子と分母のそれぞれが信号（X）に比例するので、比例分散に対応した尺度になっているとしています。 （この本では、「比例分散」という呼び方ではなく、図で説明しています。）
また、一般的な動特性のSN比は、Xの範囲を固定したデータにしないと、不都合がある点も指摘しています。

順路 次は 動特性のSN比の歴史