下のグラフは、左右共に同じデータで、 比例分散 のデータです。 左右の違いは、グラフの軸の違いで、左側は、元のデータをそのまま使っています。 右側は、X軸とY軸の両方を対数にしたグラフ（両対数グラフ）です。
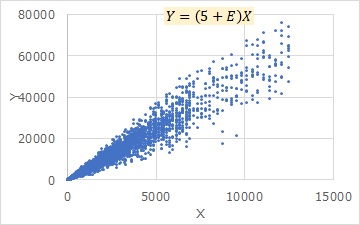
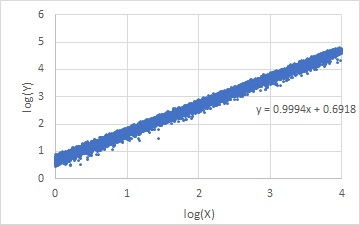
このように、両方を対数にすると、等分散（回帰直線からのばらつき方が、どのXでも等しい）のような分布に見えるので、比例分散と等分散には関係があります。 このページは、この関係の話です。
比例分散の回帰分析 に少し書いていますが、一般的には、左のグラフのようなデータに対しては、YとXの両方について対数を計算してから、 普通の回帰分析（等分散を仮定）に進む場合が多いのではないかと思います。
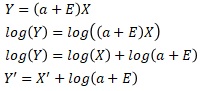
両辺を対数にすると、上のような式になります。
上の右側のグラフは、このような変換をしたX'とY'をグラフにしたものです。
このように、対数にすると、比例分散の式は、一般的な回帰分析の式に近いものになります。（logが入っているところが違うだけです。） このため、比例分散と等分散は相互変換ができます。
ちなみに、この関係は、 加法モデルと乗法モデル の関係と、とても似ています。
この変換を見ると、 X'とY'は、傾きが１で、Y切片がlog(a+E)という式になっていることがわかります。
つまり、元の比例分散の傾きがどのようなものであっても、X'とY’の関係式の傾きは１になります。
また、Y切片とY軸方向のばらつきは、log(a+E)で決まります。
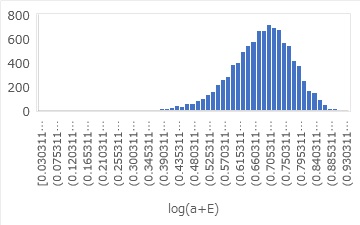
log(a+E)というのは、上のような分布です。この場合は0.69という平均値を中心にしてばらついています。 この平均値が、Y切片の値になります。 上の右側のグラフには、直線の式が計算されていて、Y切片が0.69となっていることがわかります。
このデータの場合、Eの部分は、下の図です。正規分布です。
正規分布から作られる分布にもありますが、logにすると、左右対称ではなくなり、左側の裾野が長くなっています。
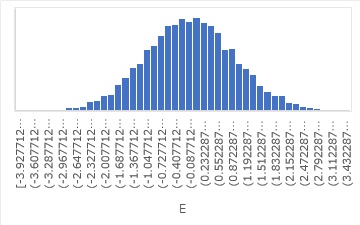
対数に変換すると、まず、傾きが必ず１になって、それ以上何も分析ができなくなります。 比例分散の時の傾きaが、対数に変換した後には、Y切片として出て来る点は、とても解釈しにくくなっています。 等分散の分析ができるのは良いのですが、その後が、とても進めにくいです。
そのため、 比例分散 のデータの回帰分析は、 比例分散の回帰分析 のページにあるように、Y/Xを計算するアプローチがベストと思います。
ただし、対数にすると、外れ値は見やすくなるようなので、その使い道はありそうです。
順路
次は
誤差の乗法モデル
