比較的新しいSN比に、エネルギー比型と変動比型があります。名前は違いますが、内容は同じようです。 「エネルギー」は、 品質工学の「エネルギー」 で、物理学的な意味ではないです。
エネルギー比型・変動比型は、全変動（Yの二乗和）を、モデルで説明できる部分と、誤差の部分に分けます。
そして、
モデルで説明できる部分 ／ 誤差の部分
のlogをSN比とします。
エネルギー比型には、n（サンプル数）の影響をなくそうとするアイディアも入っています。 変動係数を例にすると、計算の中で、分母の平均値はnで割り、分子の標準偏差はn-1で割るので、まったく同じばらつきだとしても、 nの取り方が、変動係数に影響しています。
補正の入っている計算式でも、これと同じ事情があります。 エネルギー比型のアイディアでは、「これだと、nの違う実験の比較ができない」と考えて、nやn-1で割る部分をなくすように計算しています。 （ちなみに、「n-1で割る部分をnに替える」と、意味は同じ事をしています。）
一般的な統計学では、分散は、 不偏分散 を使うべきと考えるので、n-1で割りますが、 エネルギー比型の計算では、nで割ります。 分散の推定量の議論から離れて、計算のシンプルさを優先するような方向で、データを見るようになっています。
モデルで説明できる部分 ／ 誤差の部分
の時に、「nを合わせた」というアイディアも入っていることになっています。
相関係数の２乗は、「決定係数」や「寄与率」と呼ばれます。
寄与率と呼ばれるのは、
相関係数の２乗 ＝ モデルで説明できる部分 ／ 全変動
なためです。
全変動 ＝ モデルで説明できる部分 ＋ 誤差の部分
なので、相関係数とエネルギー比型の動特性のSN比は、分析していることが似ています。
細かいところになりますが、相関係数はY切片をモデルで説明できる部分に入れるのに対して、一般的なエネルギー比型の動特性のSN比は、 Y切片の部分が誤差の方に入ります。そのため、上記の説明よりは、もう少し複雑な関係です。
品質工学がよく扱うのは、 比例分散 です。 動特性のSN比 の一般的なものは、 望目特性のSN比 からの類推で、「傾きを誤差分散で割る」という発想で作られたようです。 特に比例分散の数理的な表現が意識されていません。
下記の、エネルギー比型・変動比型の動特性のSN比や、比例分散用のSN比には、比例分散の数理的な表現としての意味がありますが、 動特性のSN比 のページにあるように、これらが測っている特徴は同じではないです。
エネルギー比型・変動比型の動特性のSN比には、比例分散の数理的な表現が当てはまるとしている文献があります。
比例分散への品質工学のアプローチ
にも書きましたが、
筆者としては、下記のSN比も比例分散用として使えると考えています。
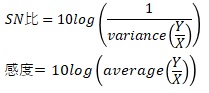
品質工学では、「X」は「M」と書くことが多いです。varianceは分散で、averageは平均です。 品質工学では、「分散」や「平均」という言葉を使わずに、その計算式を直接出すことが多いです。
比例分散用のSN比の場合は、すべての水準で比を計算してからになるので、すべての水準が平等に扱われます。 信号（X）が大きい水準の影響が大きくなることはないです。
静特性のSN比のページでは、望目特性のSN比に、「（Yの平均値 ／ Yの標準偏差）の２乗」と書いています。
一般的な解説書では、この部分を、
（Sm /n）／ Ve
、または、これをさらに補正した式で書きます。
（Yの平均値 ／ Yの標準偏差）の２乗 ＝ （Sm /n）／ Ve
なので、見た目が違いますが、内容は同じです。
Veは、不偏分散と同じで、
Ve ＝ Se ／ (n-1)
です。
ここで、
（Sm /n）／ Ve
の部分を
（Sm /n）／ （Se /n）
とすると、エネルギー比型になります。
（Sm /n）／ （Se /n）＝ Sm／Se
です。
St = Yの二乗和
で、
St = Sm + Se
なので、エネルギー比型の望目特性のSN比というのは、二乗和を分解したものの比としての意味を持っています。
単に、n-1をnに変えたものではないです。
「エネルギー比型SN比 技術クオリティを見える化する新しい指標」 鶴田明三 著 日科技連 2016
動特性のSN比のエネルギー比型について、背景にある考え方や使い方を解説した後で、静特性のSN比のエネルギー比型を解説しています。
「基礎から学ぶ品質工学」 小野元久 編著 日本規格協会 2013
変動比型のSN比が紹介されています。
変動比型の望目特性や動特性のSN比は、エネルギー比型と、定義式が同じです。
順路
次は
因子の分類
