標準偏差や分散を計算する時に出て来るのが、「分母がnか、n-1か」という話です。
教科書では、まず、分散の式としてnで割った式が出て来ます。
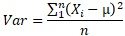
その後で、不偏分散の式としてn-1で割った式が出て来て、「基本的にこちらを使う」、という話になります。
不偏分散と対比する時は、nで割る方は「標本分散」と呼ばれます。
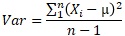
なお、「分母がnか、n-1か」が注目されがちですが、平均値も母平均か、標本平均かの違いがあります。 母平均か、標本平均かで、区別した方が、小手先の違いのように見えないので、良いようです。
標準偏差が分散の平方根であることは変わりませんが、nとn-1の話は、標準偏差にも当てはまります。
平均値の場合、定義式から計算して求めた平均値と、平均値の期待値（平均値の平均値）は同じ値になります。 平均値の平均値というのは、例えば、５個のサンプルから求めた平均値が10セットあって、その10個の平均値の平均値です。
平均値の場合は、実際に５個のサンプルから求まる平均値と、そういう平均値を集めて計算した、平均値の平均値は、少しずれます。 ずれる理由は、５個のサンプルだけの平均値の方が、計算が粗いためです。
分散の場合は、定義式（nで割る式）から計算して求めた値と、期待値（分散の平均値）が、ずれます。 ずれる理由は、５個のサンプルだけの分散の方が、計算が粗いためだけではないのがポイントになります。 平均値を計算するという操作も、ずれの原因になっています。
分散の期待値（平均値）を求めようとすると、標本分散として求めた値から、標本平均の分散を引かないと、計算が合わないということが、分散の場合は起きています。
この分散の期待値というのが、不偏分散のことです。 分散の期待値を求めることが目的なら、不偏分散を求めることになります。
統計学の一般的な解説で、標本分散を使うケースとしては、計算するデータが全数の場合を挙げています。 つまり、メンバー全員のデータが得られていて、その分散を計算する時は、標本分散を使います。 一部のメンバーのデータから、メンバー全員の分散を推定したい場合は、不偏分散を使います。
筆者の場合は、これとは異なる理由で、標本分散を使う時があります。
実務的にデータの内容を把握する時に、平均値（和をnで割った数）と同様に、「二乗和をnで割った数」や「二乗値の平均値」は参考になります。 この時に必要なのは、「二乗和をnで割った数の期待値」ではないです。「期待値」が知りたいわけではないためです。 このような時は、標本分散の計算式の方が便利です。 また、道具はシンプルな方が使い勝手が良い、という理由でも、標本分散の方が便利です。
ちなみに、ベイズ統計の参考文献には、筆者とは違う理由で不偏分散は使わない話が書かれていました。
nとn-1の違いは、分母の違いです。
例えば、nが5の場合、同じ分子について、標本分散は5で割った値で、不偏分散は4で割った値です。 標本分散の方が、4/5倍小さいということになります。
一般的には、「推定値に近いのは不偏分散。標本分散は4/5倍も違うから、その意味でも標本分散を使えない。」という説明になります。
誤解しやすいポイントですが、 「n-1になると、真の値が求まるから、n-1にする。」ではないです。 あくまで、「真の値の推定値に近くなるから」です。
結論を先に書くと、実務的には、nとn-1の違いで、何か不都合が起きることはないです。（筆者の経験の範囲ですが）
サンプル数が多いと、nとn-1の差がほとんどなくなるのは、式を見ただけでもわかります。 そのため、サンプル数が多い場合は、nとn-1の違いは気にしなくて良いです。
サンプル数が少ない場合、教科書的な説明だと、「nとn-1の違いの影響は大きい」となるのですが、実務的な観点だと、 サンプル数が少なくても、nとn-1の違いの影響は、わからないくらい小さいです。 その理由が下記の説明になります。
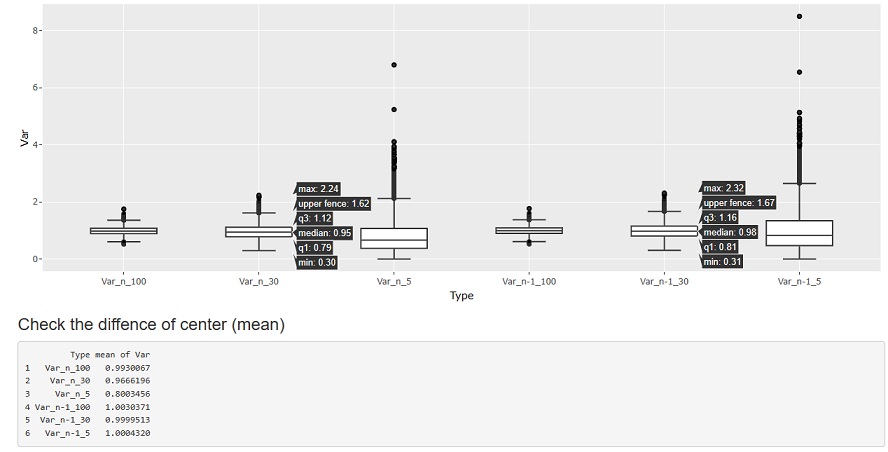
下の図は、 標準正規分布 からランダムサンプリングして、サンプル数が５個のグループを10000グループ作って、それぞれのグループの分散を計算したものです。 分散は、分布のばらつきの指標として使うのが一般的ですが、 ここでは「分散の分布」という、普段のデータ分析ではしないことを調べています。
Var_n_5とは、サンプル数が5で分母がnの標本分散、Var_n-1_5とは、サンプル数が5で分母がn-1の不偏分散です。
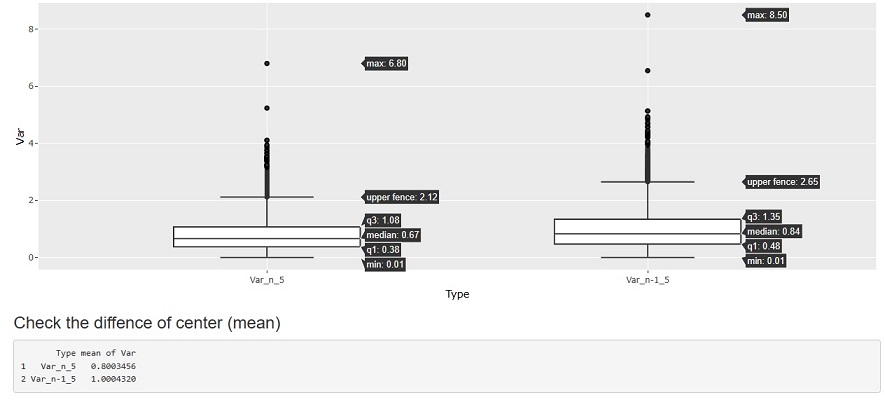
グラフの前に、下の平均値（mean）を見ると、nの方が、n-1の4/5倍（0.8/1.0）になっているので、「4/5倍も違う」という話が成り立っていることがわかります。 標準正規分布なので、真の値はちょうど1です。 n-1で計算した不偏分散の平均値は、真の値に非常に近い値が求められていることがわかります。
まず、注目すべきポイントは、ばらつきの大きさです。n、n-1に関わらず、最大値と最小値の差が7〜8くらいあります。
それだけのばらつきがあるので、平均値が0.2くらいの違いは大した違いではないです。 仮に、不偏分散と標本分散の計算を間違えたとしても、１つの分散の値を見るくらいでは、ばらつきの範囲なのか、間違えたのかがわからないほどの違いです。
n、n-1に関わらず、サンプル数が5くらいで計算した分散や標準偏差を使って、「ばらつきが変わった」という議論や、微妙な値の管理をする時の基準値としての使用は無理です。
ただし、まったく使い物にならない訳ではなく、この例では値が10よりも大きいようなサンプルに対して、「明らかに外れている」と判断する時の指標にはなります。 実務では、極端な外れ値が発生することがあるので、そのフィルターには使えます。
次に注目すべきポイントは、中央値（median）です。 この場合は、中央値は、一番出やすい値です。
これを見ると、nの場合が0.67で、n-1の場合が0.84です。 n-1の方が、真の値に近いですが、真の値と思って使えるほどの正確さはないです。 「n-1を使ったとしても、真の値よりも低い値になることが多い」とも言えます。
n-1が真の値に近いという話は、分散の平均値の話です。 実務の中では、普通は、１つの分散を計算するだけで、分散の平均値というものを計算することはないです。 分散の平均値を計算するのなら、確かにn-1でないと明確にずれますが、これを計算せず１つの分散だけで何かを進めるのなら、 そこまでn-1とnの違いは出ないです。
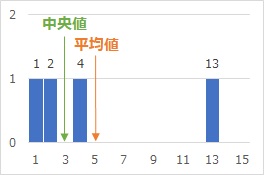
中央値が、平均値とずれているというのは、簡単な例では下図になります。
１、２、４、13というサンプルがあった時、平均値は５で、中央値は３です。
中央値は、順番に並べた時の真ん中に来ますが、平均値は左側の方がサンプルが多いです。
不偏分散は、真の値の推定値と言われていますが、真の値の推定値らしい値が出て来るのは、不偏分散をいくつか求めてその平均値を計算した場合です。 個々の不偏分散は、真の値よりも低めのものが多く計算されます。 これはこれで「バイアスがかかっている」と言って良いと筆者は思うのですが、不偏分散に対して、「バイアスがかかっている」と説明している資料を、筆者は見た事がありません。
サンプル数が30個の場合と、100個の場合も同じように調べました。
一般的に、「サンプル数が30くらいあれば、どんな分布でも正規分布とみなすことができる」、といった話がありますが、分散の議論の目安も30くらいになります。 30くらいあると、nとn-1の違いがほとんど出なくなります。 また、平均値だけでなく、中央値も、真の値にかなり近付きます。
誤差とn数 や 分散比とp値とサンプル数の関係 のページにも似たようなことを書いていますが、「分散が大きくなった（小さくなった）」という議論をするのなら、筆者の経験だと、サンプル数は100個くらいあった方が良いです。それくらいないと、調べるたびに「改善の効果があった」、「改善の効果はなかった」となって、結論が変わってしまいます。
サンプル数が100くらいあると、nとn-1の違いはほとんどないので、どちらを使っても特に不都合は起きないです。
「やさしく語る確率統計」 西岡康夫 著 オーム社 2013
分母をnにする分散の期待値を求めると、分母がn-1になる不偏分散の式が求まることが、順を追って丁寧に解説されています。
n-1にする説明として、「自由度が1少ないから」と書かれている文献を、いくつか見た事があるのですが、
その説明は、筆者にはわかりませんでした。
この本には、「分散の期待値が不偏分散」と書かれていて、その導出方法もあったので、初めてn-1が出て来る理由がわかりました。
「はじめての統計データ分析 ベイズ的<ポストp値時代>の統計学」 豊田秀樹 著 朝倉書店 2016
不偏分散を使うことが、当たり前のように言われているけれども、分散の最尤推定値は、標本分散になるので、その意味では標本分散を使うことは間違いでないことが解説されています。
また、しばしば言われている、標本分散と不偏分散の使い分けは誤りであることや、ベイズ統計では「不偏」という概念がないことも説明しています。
順路
次は
検定
