 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
ばらつきの違いの検定 の一番ポピュラーなのは、分散の比の検定(F検定)です。
「2つの平均値に違いがあるか?」ということを調べたい時は、 平均値の差の検定 にあるように「差(引き算の値)」を調べるのですが、 「2つの分散に違いがあるか?」ということを調べたい時は、「比(割り算の値)」を調べます。 例えば、グループ1の分散が、1で、グループ2の分散が3の場合、比は3になります。
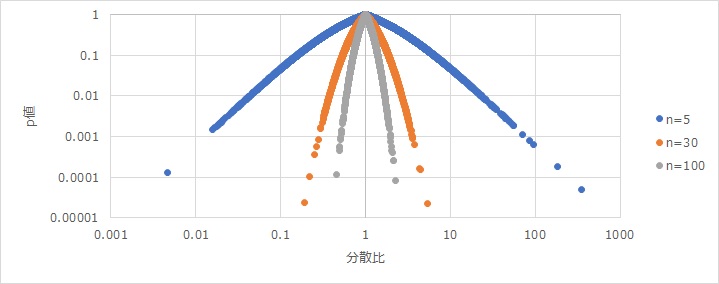
このグラフは、横軸が分散比、縦軸がF検定のp値で、サンプル数が3種類分あります。
「n=5」というのは、2つのグループのそれぞれのサンプル数が5であることを示しています。
曲線の見方ですが、まず、真ん中の分散比1のところに、頂点があり、縦軸の値は1です。 これは、分散比1が一番起きやすいことを表しています。
n=5の分散比が10あたりは、p値が0.05です。 一般的なp値の目安が0.05なので、分散比が10以上あると「2つのグループの分散は違う」と考えられるということを意味します。
例えば、「分散が5倍」と聞くと、すごい違いのように聞こえますが、それくらいでは「2つのグループの分散は違う」とは考えにくいという事も意味しています。
サンプル数nが多いと、p値は限りなく小さくなる性質があるのは、 平均値の差の検定 と同じです。
サンプル数nが多いと、分散比の大きさに関わらず、p値がとても小さな値になって、知りたいことがわからなくなります。
n=5の場合は、 正規分布になるサンプルを5個ずつ、2セット作ります。 このデータは、「=norminv(rand(),0,1)」というEXCELの関数で求めています。 ひとつのセルごとに、平均値が0、標準偏差が1に従う正規分布からランダムにサンプリングされた値が計算されます。
それぞれのセットについて、分散を計算してから割り算をして、分散比を求めます。 この値が横軸になります。
また、2つのセットの分散の比の検定をして、p値を求めます。 この値が縦軸になります。
このデータを10000通り作ります。 つまり、10000個の分散比とp値を求めます。
分散比がかなりばらついていますが、上記の方法で、10000個の分散比を作ると、このくらいばらつくのは、 筆者自身もやってみて、初めて知りました。
n=30やn=100についても同様に作ります。 あとは、グラフにするだけです。
分散は、現実には使わない単位になるので、実務のデータ分析では、ばらつきの尺度は標準偏差を使うことが多いです。
その時の目安になるように、上記の図と同様にして、標準偏差比とp値とサンプル数の関係のグラフを作ると下図になります。
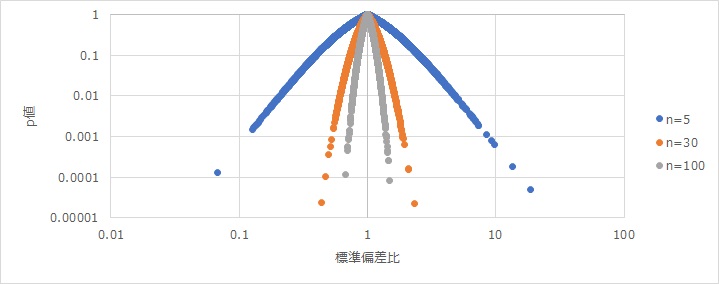
n=5だと、相当違わないと違いを判断できない点や、nが大きいと、p値が限りなく小さくなる点は分散と同じです。
このページは、p値だけの話です。 分散や標準偏差のばらつきについて、信頼区間の観点では、 誤差とn数 に説明があります。 具体的な統計量の分布の観点では、 不偏分散 に説明があります。
順路


 次は
スモールデータにおける、ばらつきの違いの評価
次は
スモールデータにおける、ばらつきの違いの評価

