分散比とp値とサンプル数の関係 のページにあるように、分散の比の検定で、「ばらつきの差がある」という結果が出るのは、 ばらつきが極端に違う時か、サンプル数が非常に多い時です。 サンプル数が非常に多い時については、「サンプル数が非常に多ければ、分散の比の検定を使っておけば良い」という単純な話ではないです。 ばらつきの違いの全体的な検定 を使う方が良いです。
サンプル数が少ない時は、ばらつきが極端に違うかを調べます。
対数を使った分析は、桁違いの違いを調べやすくする方法としても、比の評価をしやすくする方法としても便利です。
対数にするだけなので、高級感はないのですが、対数にすると良い理由は、知っていて損はない知識と思います。
対数を使うと、
例えば、
log(10) = 1
log(100) = 2
です。１桁違うと、「１」ずれるくらいの違いになります。
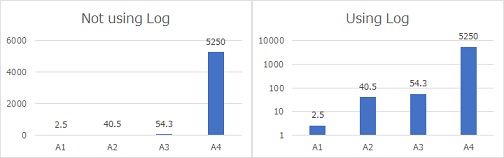
下の図の場合、左側ではA4が極端に高いことはわかるのですが、その他については違いがわかりません。 右側は同じデータを対数にしたものですが、A2とA3が同じくらいで、A1は、それらよりもさらに桁違いに小さい様子がわかります。
対数にすると、桁数が異なるデータが混ざっている場合に、桁数の違いが、見やすくなります。
例えば、棒グラフの場合、 差は、２つの棒の長さの違いとして調べられるので、グラフを見ただけでわかります。 一方、比は、長さ同士を頭の中で割り算しないとわからないです。「だいたい４倍くらいの違いかな？」といった感じで、頭の中で計算します。
話は変わりますが、
log(B) - log(A) = log(B/A)
です。
つまり、対数にした数字同士の差は、対数にする前の数字同士の比と同じです。
この性質があるので、対数のグラフで、２つの棒の長さの違いを調べることは、元のデータの比を調べることと同じになります。
スモールデータでは、桁違いにばらつきが違わないと、「ばらつきに違いがある」という結論を出すことができないです。
ばらつきの違いの検定 にあるように、ばらつきの違いを調べる時は、ばらつきの差ではなく、比を見ます。 対数による評価は、比の評価をしやすくします。 そのため、ばらつきの違いの評価で便利です。
ばらつきを対数にしてグラフにする方法は、桁違いの違いを調べやすくする方法としても、比の評価をしやすくする方法としても便利です。
上記は、「ばらつきの違いの評価は、対数を使うと良い」という話ですが、品質工学の方法論を、一般的なデータ分析の方法として、筆者がまとめ直したたものです。
品質工学 では、ばらつきの違いの評価に、昔から対数を活用しています。
品質工学 の、特徴として、 統計量 を対数（log）を使った数式で表現する点があります。
品質工学 では、対数を使う理由として、「加法性」を挙げています。 実験条件の異なるデータを、組み合わせて分析をする時に、加法（足し算）でこの計算ができるようにするため、としています。
品質工学では、検定の理論を使いません。田口先生ご自身の考え方としては、検定をしなければいけないような微妙な差は、品質の問題においては、差と見なさないところにあったようです。
（製造業で扱うようなデータは、厳密に管理されて測定されているものではないので、微妙な差は、再現性が低いです。 そのため、微妙な差で、一喜一憂することはやめ、再現性が高い明確な差だけで議論する方針が一番良いように筆者は考えます。 田口先生のお考えは、もしかしたら、このようなところから来ているのかもしれません。）
対数の使用は、サンプル数が少ないために、桁違いに違わないと、条件の影響があるとは見なせない時の方法として適しています。 さらに、比を評価する方法としても適しています。
品質工学が扱うような実験データは、サンプル数が少ないです。 また、品質工学では、ばらつきの評価が重要です。
田口先生が加法性以外の目的を意識されていたのかはわからないのですが、非常によくできた方法論になっています。
「品質工学の数理」 田口玄一 著 日本規格協会 1999
デジタルのSN比や、順位データのSN比、等の変わったSN比が紹介されている。
品質工学では、
検定
が必要ないとしている。
「製品の機能 ＝ 機能性」、ということなっている。
順路
次は
z検定による分散の比の検定
