という形をしています。
「 分散の比の検定 ＝ F検定」というのが、教科書の説明です。
F検定を使わずに、 z検定 の応用でやってしまうのが、このページの方法です。
「これで良いのでは」と筆者が考えた方法です。 z検定による分散の比の検定が必要になった経緯は、 分散比の効果量の検定 のページにあります。
z検定
は、
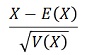
という形をしています。
これにF分布の期待値E(X)と、分散V(X)を当てはめます。Xは、分散比になるはずです。
下表に、分散比の検定のz検定版をまとめました。
分母の
は、n1=n2なら、
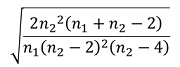
の形になります。
さらに、nが大きくなると、
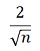
の形になります。
この式の形から、nが大きくなるとP値が限りなく小さくなる分散の比の検定の性質と合うことがわかるので、z検定版は、間違っていないのではないと筆者は考えています。
分散比の効果量の検定が、上の式で定式化できるとすれば、各種の評価指標のEXCEL関数は、 比率分布の差の効果量の検定 と同様にして、以下のようにして求まるはずです。
以下のEXCELの計算式では、以下のようになっています。
s1 ： 変数1の標準偏差
s2 ： 変数2の標準偏差
n1 ： 変数1のサンプル数
n2 ： 変数2のサンプル数
ただし、s1 > s2
任意のセルに、評価指標の計算式をコピーして、S1、S2、N1、N2のセルにこれらの数字を書いておくのが、一番簡単な使い方です。
効果量の信頼区間です。 効果量と、標準誤差を使います。
= (s1/s2)^2 - 1.96*(SQRT( (2 * n2^2 *(n1+n2-2) ) / (n1 * (n2-2)^2 * (n2-4) ) ))
NORMDIST関数の第１引数は、検定統計量です。 第２引数は、差がない事を基準にするので０です。 第３引数は、標準偏差です。
=1-NORMDIST( ( (s1/s2)^2 - n2 / (n2-2) ) / SQRT( (2 * n2^2 *(n1+n2-2) ) / (n1 * (n2-2)^2 * (n2-4) ) ) , 0 , SQRT( (2 * n2^2 *(n1+n2-2) ) / ( (n2-2)^2 * (n2-4) ) ) ,TRUE)
P値の信頼区間です。 P値の計算の効果量の部分を、信頼区間の下限に変更します。
=1-NORMDIST( ( (s1/s2)^2 - 1.96*(SQRT( (2 * n2^2 *(n1+n2-2) ) / (n1 * (n2-2)^2 * (n2-4) ) )) - n2 / (n2-2) ) / SQRT( (2 * n2^2 *(n1+n2-2) ) / (n1 * (n2-2)^2 * (n2-4) ) ) , 0 , SQRT( (2 * n2^2 *(n1+n2-2) ) / ( (n2-2)^2 * (n2-4) ) ) ,TRUE)
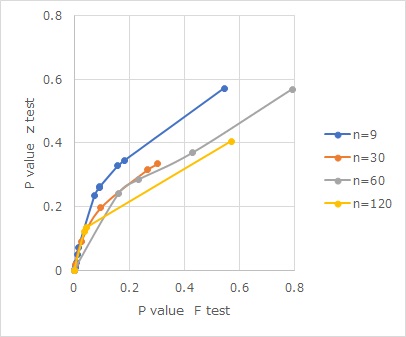
n1=n2として、nを変えつつ、F検定と比較をしてみました。
散布図の横軸がF検定のP値、縦軸がz検定のP値です。
P値が低い領域では、z検定の方がP値が２倍くらいになるようです。つまり、z検定の方が厳しめに計算されています。
「28-1. F分布」 BellCurbe 統計WEB
F分布の期待値と分散は、このサイトを参考にさせていただきました。
https://bellcurve.jp/statistics/course/9929.html?srsltid=AfmBOoq1HzCQz9lSYX7HIoVQEH9wyQbtfLqOs9sU0kuA0Vby1U2_sfFo
順路
次は
計数の差の検定
