 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
検定 には、評価の方法として、 効果量 と 信頼区間 があります。 両者は、別の考え方です。
効果量の信頼区間というのは、効果量もひとつの統計量と考えて、その信頼区間を評価に使うアイディアです。
相関係数は効果量の一種ですが、信頼区間は、 相関係数の信頼区間 に書いています。
平均値の信頼区間を標準偏差で割ることで、、効果量の信頼区間は、下記が考えられます。
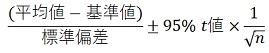
効果量の信頼区間 は、下記の参考文献にコーエンのdの効果量の信頼区間が紹介されています。
参考文献とは違うのですが、平均値の差の信頼区間から、効果量の信頼区間は、下記の式でも良いような気がしています。
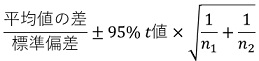
下記は、下側の求め方ですが、上側でも同様です。
EXCELの場合、例えば、差が2の場合、下の式で効果量の信頼区間(下側)が求まります。
= 2 / sqrt((n1*Var1+n2*Var2)/(n1+n2)) - 1.96*sqrt(1/n1 + 1/n2)
信頼区間は、何%の区間にするかで変わるので、その前に、効果量の標準誤差の話です。 効果量の標準誤差というのは、「効果量」という統計量の標準偏差です。
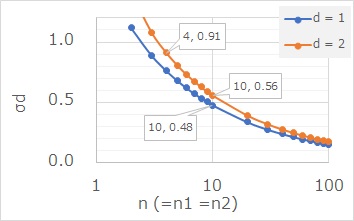
上のグラフは、コーエンのd(効果量)の標準誤差です。 参考文献の式を使って、計算したものです。 効果量が1と2の時、サンプル数と標準誤差の関係をグラフにしています。 2群のサンプル数は同じ場合の計算をしています。
このグラフの見方としては、例えば、サンプル数が10の時、効果量が1だと、標準誤差は0.48です。 効果量が2だと、標準誤差は0.56です。
d=1でも、2でも、サンプル数が100あれば、標準誤差は0.2以下です。 サンプル数が50だと、0.3以下くらいです。 このため、効果量の信頼区間を考慮しないといけないのは、サンプル数が50以下くらいのスモールデータの場合です。 それよりも大きければ、効果量の信頼区間を考慮しなかったからといって、「実は効果がないのに、効果があると判断した」という事には、とてもなりにくいです。
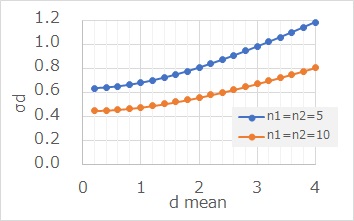
上のグラフは、サンプル数を固定して、効果量の変化に対して、標準誤差を調べたものです。
効果量の変化量に比べると、標準誤差の変化量は、数分の1くらいなので、小さいことがわかります。
信頼区間の範囲は、95%が使われることが多いですが、これは、標準誤差の約2倍(より正確には、1.96倍)です。
2倍ということは、効果量が1でサンプル数が10の場合、1を中心として、0から2の範囲が効果量の信頼区間ということになります。
効果量の平均値を固定したグラフからは、「サンプル数が10未満の時は、本当の効果量は0だとしても、計算上の効果量(効果量の平均値)は1になることがある」ということが言えるようです。
同様にして、「サンプル数が4未満の時は、本当の効果量は0だとしても、計算上の効果量(効果量の平均値)は2になることがある」とも言えるようです。
つまり、計算上の効果量が1の時は、サンプル数が10以上、計算上の効果量は2の時は、サンプル数が4以上必要です。
スモールデータの検定の効果量 のページにありますが、工場では、P値が0.05を目安にして、サンプル数が5くらいの平均値の差の検定を、今でもよくしています。 その時は、効果量が1.2くらいは確保しています。
サンプル数が5で、効果量が1.2ということは、上記の考察から考えると、信頼区間の下限が、ちょうど0くらいになります。 「サンプル数が5くらいの時、P値が0.05を目安」というのは、少ないサンプル数で汎用性・再現性の高い実験結果を得るためのギリギリのラインです。 これは、経験的に知っていた目安でしたが、効果量の信頼区間から考えても、そのくらいがギリギリのラインということがわかりました。
下のグラフは、効果量が1になる2つのグループになります。
標準偏差が1の正規分布で、平均値が1離れています。
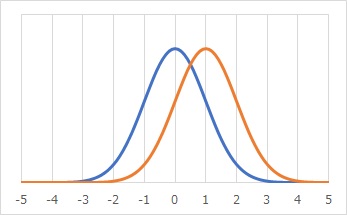
「効果量が1以上」というのは、わかりやすい目安です。 筆者の経験的にも、これくらい分布がずれていると、実務的にも経済効果が見込める量です。
効果量にもばらつきがある」という事を考慮するのなら、効果量の平均値が1では、「1くらいはずれている」とは、言いにくいです。 目安としては、効果量の信頼区間の下限が1よりも大きければ、「1くらいはずれている」と言っても良さそうな感じになります。
そこで、効果量の平均値がいくつ以上あれば、下限が1以上になるのかを調べたのが、下のグラフです。
n=5の場合は、効果量の平均値が3.0、n=10の場合は、効果量の平均値が2.2以上ないと、下限は1以上にならないことがわかりました。
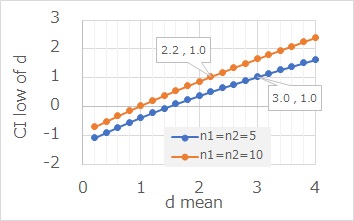
スモールデータの場合は、信頼区間が広いので、効果量の平均値は、相当大きくないと、確信を持てるような結果にならないことがわかります。
平均値の差の検定のo値B のページでは、上の調査で使ったのとは、異なる式で、効果量の信頼区間を説明しています。 平均値の差の検定のo値B のページのものをType1、 上の調査で使ったものをType2とします。
下の式は、Type2の中で標準誤差を表している部分です。Type1では、下の式の赤い四角で囲った部分がありません。
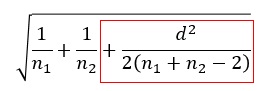
両者の違いは、下のグラフになります。
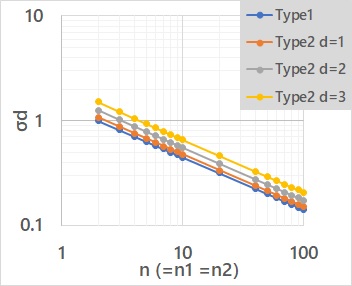
どこまで厳密さを求めるかにもよりますが、効果量で目安にすることが多いd=1の時は、ほとんど違いがないので、両者の違いは、気にしなくて良いように思っています。
「効果量も統計量なのだから、信頼区間がある」という考え方なら、コーエンのdは、従来からある検定統計量の信頼区間の一種です。
しかし、以下の2つの観点で、従来からある信頼区間とは違うようです。
コーエンのdは、標準化の処理がされた統計量なので、その点では、従来からある検定統計量とは異なります。
標準正規分布 が様々な理論を考える時に便利なように、コーエンのdには、もっと広がりのある理論になるようです。
効果量は、「データをグラフにして見えていることを定量化したもの」とも言えるので、効果量の大きさがどのくらいの確からしさなのかは、グラフを見た方が具体的にわかります。
従来からある検定統計量の信頼区間は、サンプル数に依存するため、データをグラフにしてもわからないものなので、この点が違っています。
このページは、主に平均値の差を分析する時に使われる、コーエンのdを例にして、効果量の信頼区間を考察しています。 コーエンのdの効果量の信頼区間は、まだまだ世の中で知られていないです。
ところで、2変数の関係の効果量は、例えば 相関係数 があります。 相関の検定 は、昔からあるので、相関係数の信頼区間の式は、ネット等でも簡単に調べられます。 つまり、「効果量の信頼区間」という言われ方はしませんが、相関係数の信頼区間については、古くから活用されています。
以下ページには、効果量の信頼区間の具体的な計算があります。
「効果量とその信頼区間の活用 児童心理学の進歩 2014年版」 吉田寿夫 著 金子書房 2014
特別論文Ⅲとして、この論文が含まれています。
データにはばらつきがあることを、効果量の信頼区間では考慮できるので、信頼区間を使わないよりも、豊かな情報が得られるとしています。
「本当にわかりやすいすごく大切なことが書いてあるごく初歩の統計の本. 補足2」 吉田寿夫 著 北大路書房 2018
6章が「効果量とその信頼区間の活用」です。
同著者の上記の本と、ほぼ同じ内容でした。
「心理学研究法 心を見つめる科学のまなざし」 高野陽太郎・岡隆 編 有斐閣 2017
上記の本の要点を紹介しています。
「伝えるための心理統計 効果量・信頼区間・検定力」 大久保街亜・岡田謙介 著 勁草書房 2012
3章が効果量、4章が信頼区間です。
効果量の信頼区間については、4章の終わりの方で、簡単に解説しています。
「統計検定手法の改革...その3: 効果量, 信頼区間」 西井淳 2016
コーエンのdと、その信頼区間の紹介があります。
上記の参考文献には、効果量の信頼区間の紹介はあるのですが、式が書いていないです。
筆者の試算で使った信頼区間の式は、このページを参考にしています。
https://bcl.sci.yamaguchi-u.ac.jp/~jun/post/160605-effectsize/
順路


 次は
P値と信頼区間の関係
次は
P値と信頼区間の関係

