21世紀の、比率の差の検定

21世紀の検定としての、比率の差の検定を、このページで整理します。

検定対象

２つのグループの比率の差です。

比率の差の信頼区間は以下になります。

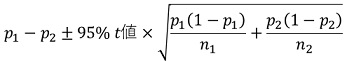
N1セルにグループ1のサンプル数、N2セルにグループ2のサンプル数、P1セルにグループ1の比率、P2セルにグループ2の比率、を入力しておくと、以下の関数はコピペで使えます。
n1　：　グループ１のサンプル数
n2　：　グループ２のサンプル数
p1　：　グループ１の比率
p2　：　グループ２の比率

下記は、下側の求め方ですが、上側でも同様です。

EXCELの場合、例えば、比率がp1とp2の場合、下の式で信頼区間（下側）が求まります。
=p1 - p2 - NORM.INV(1-0.025,0,1) * SQRT((p1*(1-p1)/n1+p2*(1-p2)/n2))

以下のどちらの関数でも、同じp値が求まります。

=1-NORM.DIST((p1 - p2) / SQRT((p1*(1-p1)/n1+p2*(1-p2)/n2)), 0, 1, TRUE)

=1-NORM.DIST(p1 - p2, 0, SQRT((p1*(1-p1)/n1+p2*(1-p2)/n2)), TRUE)

P値の信頼区間は、p値を求める式に、信頼区間の下側を入れることで、定式化してみました。

=1-NORM.DIST(p1 - p2 - NORM.INV(1-0.025,0,1) * SQRT((p1*(1-p1)/n1+p2*(1-p2)/n2)), 0, SQRT((p1*(1-p1)/n1+p2*(1-p2)/n2)), TRUE)

比率の差の検定は、平均値の差の検定と似た形で検定をします。そのため、効果量についても、同様に考えるのなら、以下で良いと考えられます。

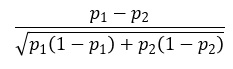
= (p1 - p2) / SQRT(p1*(1-p1)+p2*(1-p2))

比率の比や、オッズ比も、効果量として良さそうです。

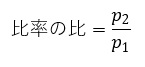
=p2 / p1

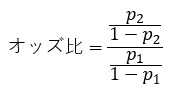
=(p2 / (1-p2)) / (p1 / (1-p1))

個別の比率の信頼区間は、以下のようになっています。

=p1 + NORM.INV(1-0.025,0,1) * SQRT(p1*(1-p1)/n1)
=p1 - NORM.INV(1-0.025,0,1) * SQRT(p1*(1-p1)/n1)

効果量の信頼区間は、これを効果量の式に使えば良いと考えられます。

p1の方がp2よりも高いことを検証したい場合、
p1 > p2
だったとしても、
p1の信頼区間の下側 < p2の信頼区間の上側
になっていないかが、最初の確認点です。

次に、p1の信頼区間の下側と、p2の信頼区間の上側を使って効果量を計算した時が、効果量の信頼区間の下側になり、これがある程度確保できていないと、「効果がある」とは考えられなくなります。

例えば、効果量を比率の比にする場合の、効果量の信頼区間の下限は、以下になります。
= (p2 + NORM.INV(1-0.025,0,1) * SQRT(p2*(1-p2)/n2)) / (p1 - NORM.INV(1-0.025,0,1) * SQRT(p1*(1-p1)/n1))

寄与率は、以下のようにして計算します。

比率を計算する前の元データを、以下のように加工します。 Zを使って、グループの違いを表します。１と０は逆でも問題ありません。
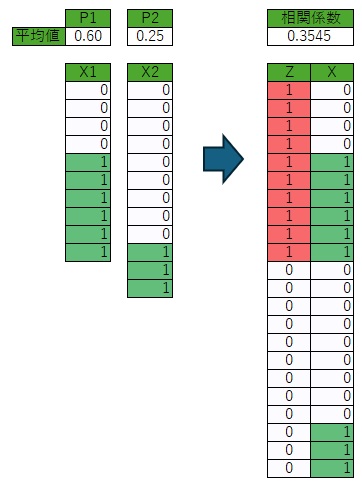
o value

ここまで準備できると、ここからは、平均値の差の検定の寄与率と基本的に同じです。相関係数rを求めます。

寄与率は、相関係数の二乗です。
=r1^2

寄与率の信頼区間（上側）です。相関係数の検定にある信頼区間を使います。

= (( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) +1))^2

相関係数の検定のo値のページにまとめています。

「21-6. 母比率の差の信頼区間」　BellCurbe 統計WEB
母比率の差の信頼区間は、このサイトを参考にさせていただきました。
https://bellcurve.jp/statistics/course/18452.html?srsltid=AfmBOorEgW6RxFd4j1pK8EAUpshCQGVFgvUrhcZcHNOoSrg-tdwpAM8J

「21-1. 母比率の信頼区間の求め方1」　BellCurbe 統計WEB
母比率の信頼区間は、このサイトを参考にさせていただきました。
https://bellcurve.jp/statistics/course/9122.html?srsltid=AfmBOoorHFHf1Q7nW2Es29kwKcEkbP-SRDHJ-lSQhVrjYPVgix7kOSMb