21世紀の検定 としての、 平均値の差の検定 を、このページで整理します。
２つのグループの平均値の差です。
平均値の差の検定では、信頼区間が下記の式になっています。
95% t値というのは、サンプル数で変わりますが、約２です。
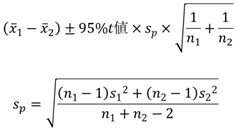
以下では、グループ1の方が平均値が高いことの検証を想定します。 また、いずれの平均値も正の値を想定します。 高低が異なる場合や、負の値の場合は、以下の式を応用します。
実務で信頼区間として知りたいのは、平均値の差がどのくらいまで低い可能性があるのかなので、 以下では、上の場合は、信頼区間の下側が知りたいことになります。 このページの他の信頼区間についても同様です。
平均値差の差の信頼区間の下側の具体的な計算は、以下になります。
D1セルに平均値の差、N1セルにグループ1のサンプル数、N2セルにグループ2のサンプル数、S1セルにグループ1の標準偏差、S2セルにグループ2の標準偏差、を入力しておくと、以下の関数はコピペで使えます。
d1 ： 平均値の差
n1 ： グループ１のサンプル数
n2 ： グループ２のサンプル数
s1 ： グループ１の標準偏差
s2 ： グループ２の標準偏差
=d1 - T.INV.2T(0.05,n1+n2-2) * SQRT(((n1-1)*s1^2+(n2-1)*s2^2) / (n1+n2-2)) * SQRT(1/n1+1/n2)
以下のどちらの関数でも、同じp値が求まります。
=T.TEST(グループ1のデータの範囲, グループ2のデータの範囲, 2, 2)
=T.DIST.2T(d1/(SQRT(((n1-1)*s1^2+(n2-1)*s2^2) / (n1+n2-2)) * SQRT(1/n1+1/n2)), n1+n2-2)
P値の信頼区間 は、標準偏差の信頼区間 を以下の形に変形して使えば良いと考えています。
以下の式をV1セルに書くと、V1セルに、合成した分散の信頼区間の上側が入ります。
=(n1+n2-1) * (((n1-1)*s1^2+(n2-1)*s2^2) / (n1+n2-2)) / CHIINV(0.975,n1+n2-1)
p値の信頼区間の上側は、V1セルを読み込みます。
=T.DIST.2T(D1/(SQRT(V1) * SQRT(1/N1+1/N2)), N1+N2-2)
平均値の差の検定の効果量は、「コーエンのd」や、「ヘッジのg」と呼ばれているものがあります。
式は、平均値の差を、標準偏差で求める形です。
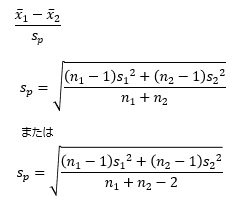
p値を求める時に使う、t値と、とても似ています。
=d1 / SQRT(((n1-1)*s1^2+(n2-1)*s2^2) / (n1+n2-2))
効果量の信頼区間
は、平均値の差の信頼区間との対応から、以下で良いと筆者は考えています。
=d1 / SQRT(((n1-1)*s1^2+(n2-1)*s2^2) / (n1+n2-2)) - T.INV.2T(0.05,n1+n2-2) * SQRT(1/n1+1/n2)
寄与率
は、以下のようにして計算します。
分母は、すべてのデータについて、すべてのデータの平均値との差の、二乗和です。
分子は、分母の平方和から、各グループの平均値の、全体の平均値からのばらつきの分です。
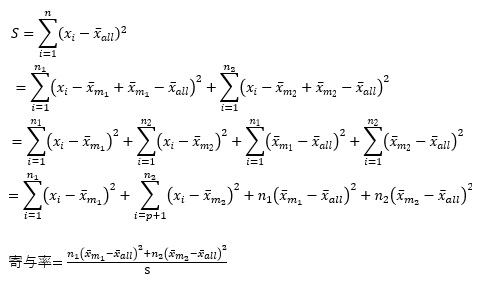
上の式を計算しても良いのですが、データを以下のように変形して、ZとXの相関係数の二乗を計算しても、寄与率が求まります。
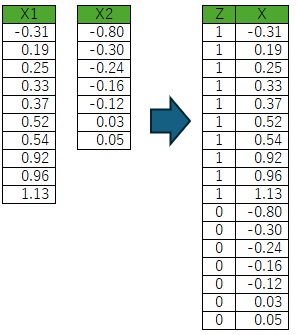
=CORREL(Zの範囲, X範囲)^2
寄与率を相関係数を使って求めるようにすると、寄与率の信頼区間は、 相関係数の検定 にある寄与率の信頼区間が使えます。
N1セルにサンプル数（２つのグループの合計サンプル数）、R1セルに相関係数、R2セルに以下の式を入力しておきます。
= ( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+r1)/(1-r1) ) -2*1.96/SQRT(n1-3) ) +1)
相関係数の信頼区間の下側は、以下の関数で求まります。
=r2^2
平均値の差の検定のo値 のページにまとめています。
順路
次は
平均値の差の検定のo値
