 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて |
ENGLISH
相関係数については、相関係数の数値的な確かさの調査が、従来からある 相関係数の検定 になります。
相関係数の検定 でp値が低いということは、「相関係数の精度が高い」という意味です。 そのため、 相関係数の検定 のp値は、相関の高さとは無関係な指標です。
例えば、相関があるとは言えない場合でも、 相関係数の検定 のp値が、限りなく0に近くなることがあります。 よって、相関があるかないかという指標として、 相関係数の検定 のp値は使えないです。
一般的な研究では、相関がどのくらい確からしいのかを確率の指標で評価したいことが多いと思います。 さらには、その指標の確からしさもわかると、なお良いです。
相関係数の検定のo値は、その目的に使います。
なお、相関性を寄与率にして確率的に評価する方法は、昔からあります。 しかし、この指標を「検定」として考える発想は、従来はないと思いますので、「古くて新しい方法」と言えそうです。
o値Aの方が、高めになります。
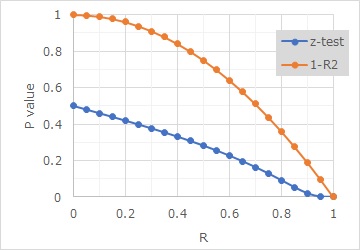
寄与率法は、相関係数には、2乗すると寄与率という確率になる特徴が、もともとあるので、そこから定式化しています。
=1- R1^2
o値の信頼区間(上側)です。 相関係数の信頼区間 を使います。
=1-( ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1) )^2
上の式の場合、相関係数Rが0.9だと、o値は、0.19(= 1- 0.9^0.9)になります。
この0.19というのは、「完全な直線上で相関する場合に対して、未知の要因が0.19(19%)ある」という意味になります。 「未知の部分が19%しかない」と解釈すれば、「かなり高い相関」という意味になります。
z検定法は、 平均値の差の検定のo値B と同様で、検定統計量を変形することで定式化しています。 なお、ここでは、(n-2)の部分を取ることで、定式化しています。 これによって、nに依存しない検定統計量になっていますが、単純に(n-2)を取るのではない方が、もしかしたら良いのかもしれません。
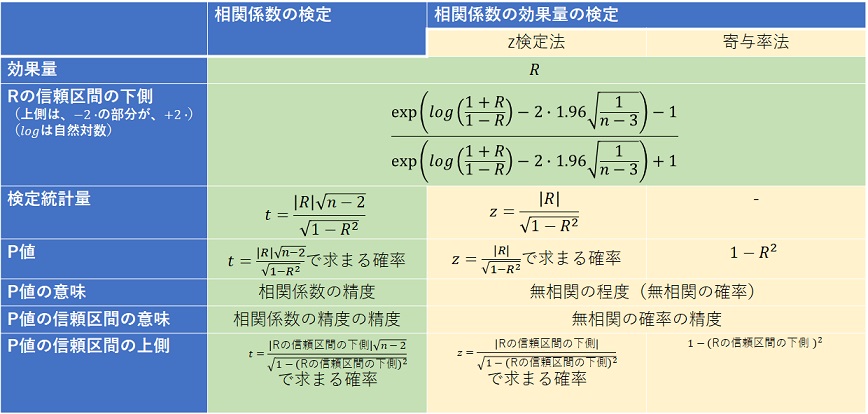
=(1 - NORM.DIST(R1/SQRT(1-R1^2),0, 1,TRUE)) *2
o値の信頼区間(上側)です。 相関係数の信頼区間 を使います。
=(1 - NORM.DIST((( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1))/SQRT(1-(( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) -1) / ( EXP(LN( (1+R1)/(1-R1) ) -2*1.96/SQRT(n1-3) ) +1))^2),0, 1,TRUE)) *2
「26-3. 相関係数」 BellCurbe 統計WEB
相関係数の信頼区間は、このサイトを参考にさせていただきました。
https://bellcurve.jp/statistics/course/9591.html?srsltid=AfmBOooI8DcFdnGNYGJ0lRux7v-MC64V-RZLTI4JSynm0g6M6IGnEOfB
順路


 次は
21世紀の、平均値の差の検定
次は
21世紀の、平均値の差の検定

