21世紀の検定 としての、 分散の比の検定 を、このページで整理します。
２つのグループの分散の比です。
分散の比の検定では、信頼区間が下記の式になっています。
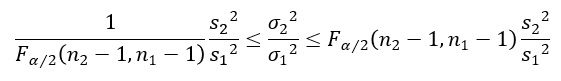
信頼区間の上側の具体的な計算は、以下になります。
N1セルにグループ1のサンプル数、N2セルにグループ2のサンプル数、S1セルにグループ1の標準偏差、S2セルにグループ2の標準偏差、を入力しておくと、以下の関数はコピペで使えます。
n1 ： グループ１のサンプル数
n2 ： グループ２のサンプル数
s1 ： グループ１の標準偏差
s2 ： グループ２の標準偏差
=F.INV.RT(0.05/2,N1-1,N2-1) * (S2/S1)^2
信頼区間の下側は、以下になります。
=(1/F.INV.RT(0.05/2,N1-1,N2-1)) * (S2/S1)^2
以下のどちらの関数でも、同じp値が求まります。
=F.TEST(グループ1のデータの範囲, グループ2のデータの範囲)
=F.DIST(MIN((s2/s1)^2, (s1/s2)^2), n1-1, n2-1, TRUE) *2
分散の比は、分散に違いがなければ１に近くなります。 この点が、差を評価する検定とは異なります。
実務の分析では、現状の分散があり、対策をすることで、分散が小さくなることを狙うテーマが多いです。 以下では、グループ1の方が分散が大きいことを想定します。 従って、分散の比は1よりも小さく、分散の比が小さければ小さいほど、違いが大きいことを想定した分析をします。
このようなテーマでは、分散の比の信頼区間の上側の場合に、 P値の信頼区間 がどうなるのかを調べたいです。
以下では、p値を求める式に、分散の比の信頼区間の上側を入れれば、p値の信頼区間になると考え、定義してみました。
分散の比が１よりも小さい場合でも、信頼区間の上側が１よりも大きくなる場合があります。 １よりも大きくなる場合は、「効果なし」と同じなので、１以上はすべて１とします。 この計算が、以下のMIN関数の中に入っています。
=F.DIST(MIN(F.INV.RT(0.05/2,N1-1,N2-1) * (s2/s1)^2, 1), n1-1, n2-1, TRUE) *2
分散の比の効果量は、世の中にないようです。
他の検定の効果量は、無次元数である特徴から類推すると、分散の比の効果量は、分散の比が適当と考えられます。
分散の比の効果量を、「分散の比」と考えるのなら、 効果量の信頼区間 は、分散の比の信頼区間と同じで良いと考えられます。
そこから類推すると、分散の比の寄与率は、以下のように考えます。
ただし、グループ1の方が分散が大きい前提です。
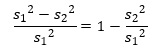
= 1- (s2/s1)^2
寄与率の信頼区間（上側）です。
MIN関数を使う理由は、上記のp値の信頼区間と同じです。
=1 - MIN(F.INV.RT(0.05/2,N1-1,N2-1) * (s2/s1)^2, 1)
分散の比の検定のo値 のページにまとめています。
「28-3. 母分散の比の信頼区間の求め方」 BellCurbe 統計WEB
母分散の比の信頼区間は、このサイトを参考にさせていただきました。
https://bellcurve.jp/statistics/course/24270.html
順路
次は
分散の比の検定のo値
