トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

検定

平均値 を比べて、「こっちが高い」と結論を出すのは、よくある話です。 しかし、データが大きくばらついている場合、 「この平均値の差は、偶然かも。。。」という疑いが出て来ます。

分布のグラフ を見ることでも確認できますが、 サンプルが少ない時や、差が微妙な時は、グラフの見た目ではよくわからない時もあります。

こういう時に、 統計学 を使って、差の有無を調べる方法は、「検定」と呼ばれています。 「検定」の考え方は、 異常値の判定 でも役に立ちます。

検定の基本的な考え方（有意水準とP値）

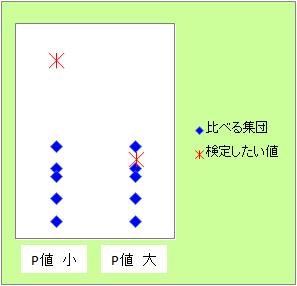
検定の方法は、平均値や分散等、いろいろな統計量に対してあります。 途中で使う分布が違ったりするものの、 どの統計量の話も、最終的には図のような形にして検定します。

左の場合のように、検定したい値が、比べたい分布の中心に近ければ、分布の仲間と考えやすいです。 一方、分布の中心から遠ければ、分布の仲間とは考えにくいです。

検定では、「近い」や「遠い」とは言わずに、「有意な差がある」と言います。 有意な差があるかどうかの基準を、有意水準といいます。

集団との関係の尺度が、P値（ピーチ）です。 遠い場合は、P値は小さくなります。

一般的には、有意水準は0.05（5%）を目安にすることが多いです。
「P値が0.05よりも小さい」　
＝　「考えにくいことが起きている。」　
＝　「有意な差がある。」
、と考えます。

検定の誤用を避けるため

検定の誤用については、様々なことが言われていますが、根本的な注意点は、以下になります。

従来からある検定手法は、データのばらつきを考慮する手法になっていない

例えば、平均値の差の検定では、「平均値に差があると言えるか？」ということだけが調べられます。 データにはばらつきがあるので、２つのグループに違いがあるかどうかは、データのばらつきも踏まえて考察しないといけないことが多いですが、 平均値の差の検定は、それを調べられるように作られていません。

それにも関わらず、従来からある検定手法を使うことで、様々な混乱が生まれています。 そのための対策も生まれていますが、対策の使いこなしよりも、目的と手段の不一致をなくす方が、根本的な対策になります。

従来からある教科書では、この点があいまいになっているので、目的と手段の不一致が起こっている研究が非常に多いようです。

対立仮説がいらない研究もある

帰無仮説と対立仮説の両方を明確に設定しなければいけないのは、ネイマン・ピアソン流の検定を使う場合です。

従来からある教科書では、検定では、 第１種と第２種の誤り の可能性が、必ずあるように書かれているものが多いようですが、第２種を考えなければいけないのは、ネイマン・ピアソン流の検定を使う場合だけです。

また、同様にして、検出力を考慮する必要があるのも、ネイマン・ピアソン流の検定を使う場合だけです。

フィッシャー流と、ネイマン・ピアソン流の使い分け

「 統計的な検定と、統計教育の歴史 」のページに、やや詳しく書きましたが、世の中での検定の解説では、フィッシャー流と、ネイマン・ピアソン流が混同されていることが、とても多いです。

このサイトでは、区別するようにしています。 このページは、1-1-3ですが、1-1-3-0から1-1-3-7までは、フィッシャー流の話です。 1-1-3-8の、 ネイマン・ピアソン流の検定 だけが、ネイマン・ピアソン流です。

なお、２つの流派を混同するのは、このサイトも例外ではないです。 混同していることに気付いたのは、2024年です。 気付いてからは、修正を進めていますが、もしかしたら、混同してしまっている説明が残っているかもしれません。 （気付いた方は、ご連絡いただけると幸いです。）

21世紀の検定

ノンパラメトリック検定 のページにまとめましたが、ノンパラメトリック検定も含め、従来の検定手法は、すべて、統計量の分布を使う方法（統計量の数値のみを見る手法）として開発されて来ています。

「検定とは、そういうものだ」という考え方もできるかもしれませんが、そうだとすると、様々な分野で研究手段として使えないです。 言い換えれば、ニーズに合っていないです。

21世紀の検定 は、「ニーズに合う検定手法」や「目的に合う手段」として、筆者が体系を見直したものです。 必要な手法なのに、ないものについては、筆者が考案しています。

新たに追加した手法は、統計量の分布ではなく、データの分布について、P値を計算する点が共通しています。

検定で、一番大事な事は何ですか？

参考文献

「P値　その正しい理解と適用」　柳川堯　著　近代科学社　2018
P値はサンプルサイズに依存するので、P値の大きさだけで仮説の判断ができない事の他に、サンプルサイズが小さい時には、P値のばらつきが大きいので、これだけで判断するのは良くないことを指摘しています。
・探索的な研究の時には、フィッシャー流の検定が良い。P値はエビデンスの強さの指標であり、判定の指標とは考えない。判定は、他の観点を踏まえて行う。
・検証的な研究の時には、ネイマン・ピアソン流が良い。サンプルサイズを事前に設定する。
・メタアナリシスとして、複数の異なる実験を統合した時のP値の計算法がある。
・多重性を調整するためのP値がある。

「p値とは何か　統計を少しずつ理解する34章」　Andrew Vickers　著　丸善出版　2013
タイトルからは、P値を中心に解説した本のように見えましたが、統計学全般の入門書として書かれています。
・サンプルサイズの設計については、統計学的な観点よりも、コストや倫理の観点で、サンプル数を増やしにくい場合に、実験で確認したいこととのバランスを取るために必要

「統計解析がわかる」　涌井良幸・涌井貞美　著　技術評論社　2020
筆者が見たことがある中で、初学者向けでも、内容がきっちり書かれている本です。

順路 次は 検定による判断