第１種と第２種の誤り

ネイマン・ピアソン流の検定では、第１種の誤り（第１種の過誤）と、第２種の誤り（第２種の過誤）と呼ばれるものがあります。

第１種の誤り

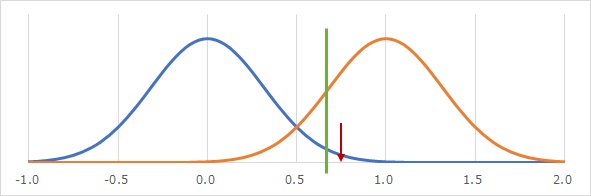
帰無仮説が青色の分布で、対立仮説がオレンジ色の分布だったとします。いずれも平均値の分布です。しきい値は、緑色の線の値とします。

そして、測定したデータで求めた平均値が0.75で、赤い矢印の位置だったとします。この場合、「データは、帰無仮説の分布には属さない」と判断するのが、検定の手順です。

ところが、「データは、帰無仮説の分布には属さない」と判断したけれども、測定したデータがたまたまそうだったからで、真の値は、帰無仮説の分布だった場合が、第１種の誤りです。

第１種の誤りは、検定による判断の弱点と似ています。

第１種の逆もあります。

対立仮説として設定した分布について、しきい値を超えたので、「対立仮説の分布には属さない」と判断したのに、真の値は、対立仮説の分布だった場合が、第２種の誤りです。

ラベル分類の方法で使われる偽陽性・偽陰性と、第１種、第２種の誤りは共通点と、相違点があります。

世の中の解説では、「これは混同してしまっているのでは？」と思われるものが、時々、見かけます。（今は、なくなっているはずですが、このサイトでも、過去に混同している説明がありました。）

推定と実際が違っていたことを見ている点は、共通しています。

第１種・第２種の誤りの話は、２つの分布の絵で説明されることが多いですが、この分布は、統計量の分布です。

平均値の差の検定や比率の差の検定のような有名な検定は、統計量の分布を調べる方法なので、統計量の分布の話になっています。

一方、偽陽性・偽陰性は、個々のサンプルの分布についての話です。