帰無仮説が青色の分布で、対立仮説がオレンジ色の分布だったとします。 α（アルファ）とβ（ベータ）と呼ばれるものは、しきい値を決めた時に、上の図で表されるものです。 いずれも面積のことで、この面積が確率を表しています。
第１種と第２種の誤り とセットになっているのが、有意水準と検出力とサンプル数です。
まず、誤解しやすいところですが、有意水準と検出力とサンプル数の話は、実験前に決まって来る話です。 データ分析の手法ではないです。
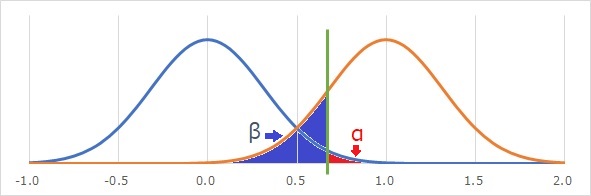
帰無仮説が青色の分布で、対立仮説がオレンジ色の分布だったとします。
α（アルファ）とβ（ベータ）と呼ばれるものは、しきい値を決めた時に、上の図で表されるものです。
いずれも面積のことで、この面積が確率を表しています。
αは、「有意水準」とも呼ばれます。 αは、第１種の誤りになる確率です。
βは、第２種の誤りになる確率です。
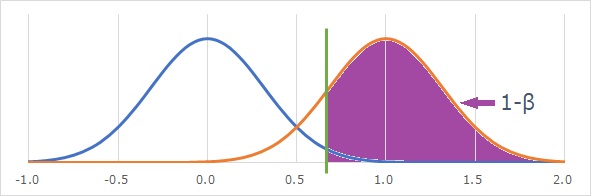
１−βは、「検出力」と呼ばれます。
２種類の対立仮説 のページでは、世の中の対立仮説には、大きく分けると２種類があることを説明しています。
図を見ればわかるように、有意水準と検出力の両方の話をするには、分布が２つ必要です。
「対立仮説とは、帰無仮説と論理的に逆のもの」の場合、分布は１つしか想定していないのですが、有意水準と検出力の両方の話が出て来る文献があります。
このような文献の場合、対立仮説の書き方は、「平均値は１よりも大きい」になっているのですが、 実際に計算する時には、対立仮説の方は、例えば、「平均値は２、標準誤差が１の正規分布」と読み変えています。
読み変える時には、扱っているテーマからの要請で決める方法もありますが、統計学的な決め方としては、 効果量 の考え方を使って、対立仮説を決める方法があります。 例えば、「対立仮説は、平均値の差が、標準偏差よりも大きい」といった基準から決めます。
まず、仮説として、２つの分布の形と、平均値、標準偏差を仮定します。
次に、有意水準（α）と検出力（１−β）の設計は、まず、しきい値の位置の設計になります。 しきい値の位置によって、αとβの両方が変わります。
一般的な目安としては、「αは0.05以下、βを0.2以下（つまり、検出力が0.8以上）」があります。
ここでひとつ複雑なことがあります。 標準誤差は、サンプル数が多いと小さくなる性質があるので、 単純にαとβを小さくしたいなら、しきい値の調整は不要で、サンプル数を増やせば良いだけです。
しきい値の調整が必要になってくるのは、サンプル数を増やすことにコストや倫理的な問題があって、少しでもサンプル数を減らしたい時です。
「サンプルサイズの決め方」 永田靖 著 朝倉書店 2003
平均値の検定、平均値の差の検定、分散の比の検定、など、一般的な検定について、
統計学的な決め方で、対立仮説を決める方法を紹介しています。
例えば、平均値の検定は、帰無仮説にt分布を使った場合、対立仮説仮説には非心t分布を使います。
F分布の場合は、非心F分布です。
筆者としては、非心の分布でなくても良いように考えているのですが、「帰無仮説に相当する分布がある前提での、対立仮説の分布」ということを扱おうとすると、非心の分布になるようです。
順路
次は
２群の検定の対立仮説
