２群の検定の対立仮説

有意水準と検出力とサンプル数の理論は、１群の検定についての説明になっています。

「２群の場合は、どうなのか？」このページの話です。

１群の検定の手順

ここで１群の検定の手順を考えてみます。詳しくは、有意水準と検出力とサンプル数にあります。

１群の検定では、データは、１群のものです。一方、仮説にする分布は、帰無仮説用・対立仮説用の２つがあります。

１群の検定は、「データは、２つの分布のどちらに近いのか？」という方法として作られています。

２群を扱う検定としては、平均値の差や、分散の比の検定などがあります。

平均値の差の検定は、「平均値の差」という量のばらつきを調べる方法として、作られています。そのため、分析の最初では２群を扱っていますが、途中から１群の検定（平均値の検定）と同じ手順になっています。

平均値の差の検定を、フィッシャー流で進める場合、帰無仮説は「差が０」、対立仮説は「差が０ではない」となります。

ネイマン・ピアソン流で進める場合、帰無仮説は「差が０」、例えば、対立仮説は「差が１」となります。

分散の比も、同様で、途中から１群の検定になります。仮説の置き方は、平均値の差の検定と同様です。

平均値の差の検定の仕組みでは、平均値の差の検定の理解の仕方として、２通りを説明しています。上記で説明したのは、教科書的な説明の方です。 t検定やz検定を使います。

直観的な説明の方の場合、データが１群にまとめられていないです。

データが２群ある場合、帰無仮説は「２群は同じ」、対立仮説は「２群は異なる」になります。

この場合の検定の方法としては、分散分析が開発されています。

２群を２群のまま分析するアプローチの場合、サンプル数の決め方が簡単です。信頼区間・標準誤差から決める方法の一種になります。

例えば、「平均値の差が、標準誤差より大きければ、有意とする」と決めるのなら、

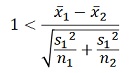
に平均値の差と、標準偏差を代入すれば、サンプル数が求まります。

例えば、平均値の差が１で、標準偏差が両方とも１で、サンプル数が同じなら、右辺は、

１／（２／サンプル数の平方根）

です。よって、　

サンプル数　＞　4

という数字が出て来ます。

上の例の場合、群１、群２について、それぞれサンプルを４つずつ用意して、平均値と標準偏差を求めます。

（群１の平均値　－　群２の平均値）／（群１の標準偏差／群１のサンプル数の平方根　＋　群２の標準偏差／群２のサンプル数の平方根）

を計算した時に、１よりも大きい数字が出た場合、「サンプル数が大きかったから」という可能性は排除できます。

平均値の差が大きかった可能性と、標準偏差が小さかった可能性だけになります。

「サンプルサイズの決め方」　永田靖　著　朝倉書店　2003
平均値の検定、平均値の差の検定、分散の比の検定、など、一般的な検定について、統計学的な決め方で、対立仮説を決める方法を紹介しています。