平均値の差の検定の仕組み

平均値の差の検定のページで、「平均値の差の検定の仕組み」としている説明は、直観的な理解をしやすいようにアレンジしたものになっています。

教科書的な説明を知っていた方が良い事もあるので、このページでは、教科書的な説明をまとめています。

教科書的な説明

教科書のような解説をすると、以下になります。

まず、スタートになる数式です。平均値を標準誤差で割る事を表しています。意味は、標準化された平均値の分布です。差を見るので、X1とX2の差が式の中に入っています。

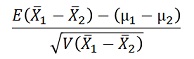
これを期待値の公式を使って変形させます。μというのは、真の値です。差の検定では、真の値が等しいと仮定するので、式が簡単になります。

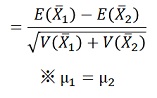
さらに変形させます。ここで、分母は、２つの分散をひとつに扱えるようにするためのものを定義しています。平均値の分散なので、σの２乗をnで割った式になっています。

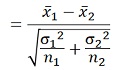
考察をしやすくするために、２つの群のサンプル数が等しい場合を想定すると、式がさらに簡単になります。

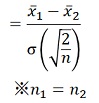
上の式は、いわゆる「分散が既知の場合」です。未知の場合は、σと書いていたところが、s（標本標準偏差）に変わるだけでなく、t分布も使うので、式が複雑になります。

平均値の差の検定では、上の式で表される量が、標準正規分布のどの位置なのかを調べます。

すると、確率的に起きやすいのかどうかが定量的に表せるようになります。このような仕組みになっています。

なお、「標準正規分布」という表現は、正確ではないです。平均値の差の検定では、「母分散が未知」ということを考慮して、t分布で進めます。 t分布は、母分散が未知の場合に、未知の要因によるばらつきが考慮できるように作られた分布になっています。

平均値の差の検定では、２群を扱いますが、上手にまとめることで、１群の検定に帰着させています。

「２群の検定は、１群の検定の形にして進める」、という説明の仕方は、教科書にあるような説明の仕方です。数式はそこから導かれています。

ところが、できた式を見てみると、これは、
平均値の差／（標準偏差／サンプル数nの平方根）
という形をしています。

「「平均値の差は、平均値の分布のばらつきが何個分か？」ということを、評価する方法」と理解しても、間違いではないことがわかります。

平均値の差の検定のページの説明は、このような解釈の元で、書かれています。

効果量「平均値の差は、平均値の分布のばらつきが何個分か？」ではなく、「平均値の差は、データの分布のばらつきが何個分か？」という似た考え方で作られています。

機械学習のラベル分類では、２群がある時、素直に２群を扱います。１群の問題にまとめたりしないです。

平均値の差の検定を、２群のまま定式化したものとして解釈しておくと、機械学習の分野との関係がわかりやすくなるようです。

２群を１群として考えると、対立仮説として、例えば、「平均値の差が５のグループに入るのか？」といったことを想定して、計算することになります。しかし、平均値の差の検定で扱いたいのは、「５以上と言えるのか？」や、「５以上のグループに入ると言えるのか？」なので、目的と手段が合わないです。

こんなことが起きるのは、１群として考え始めたことに原因があります。詳しい話は、２群の検定の対立仮説のページにあります。