トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

平均値の差の検定の、p値とサンプル数の関係

平均値の差の検定をする時に、教科書には「p値は0.05を目安に」と書かれているにも関わらず、サンプル数が多い時は0.05よりもはるかに小さな値が、普通に計算されて、「？」となることがあります。

サンプル数の影響

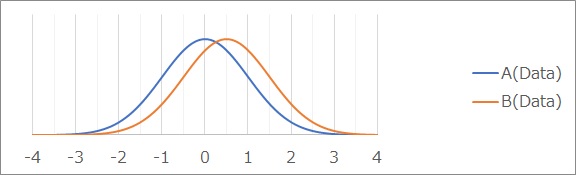
上のように２つのグループがあったとします。グループAの平均値が０で、Bの平均値が0.5です。 それぞれ標準偏差は、ちょうど１です。

上のデータについて、平均値の分布のグラフを作ります。 平均値、標準偏差、サンプル数の３つを使います。　 サンプル数が、10000のデータを使っている場合です。

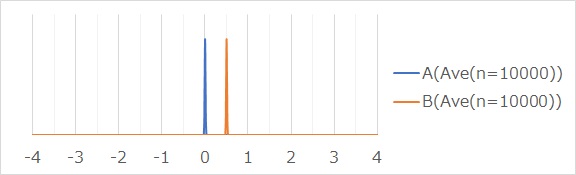
平均値と標準偏差は同じでも、サンプル数が３の場合は、下のようになります。

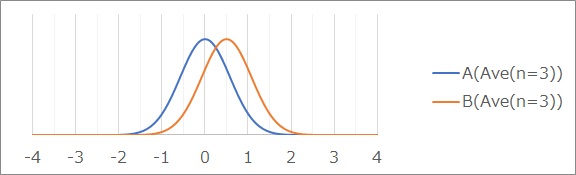
サンプル数が10000の場合は、「２つの平均値は明確に異なる」と言えます。 一方、サンプル数が３の場合は、「異なるかもしれないが、明確ではない。」となります。

元のデータから推測される分布が同じだとしても、サンプル数が多ければ、明確な判断ができるようになるのが、平均値の差の検定の特徴です。

サンプル数nが多いと、p値が限りなく小さくなる理由

平均値の差の検定の計算で使われている統計量は、ざっくり見ると、以下の形になっています。 この計算をすることで、２つの平均値の差と、２つの平均値のそれぞれの幅の関係を調べられるようになっています。
平均値の差／（標準偏差／サンプル数nの平方根）

これは、変形すると以下になります。
平均値の差／標準偏差＊サンプル数nの平方根

平均値の差、標準偏差、サンプル数nの平方根の３つの要素の内、nの変化によって、桁違いに変化することがあるのは、 サンプル数nの平方根の部分だけです。 そのため、この統計量は、サンプル数nの影響を大きく受けます。

特に、nがある程度以上になると、平均値の差と標準偏差の値はほとんど関係がなくなって、nの影響だけでこの統計量が決まるようになります。 nが多ければ多いほど、この統計量は限りなく大きくなります。 そのため、p値が限りなく小さくなります。 これが、サンプル数nが多いと、p値が限りなく小さくなる理由です。

サンプル数nが多いと、p値が限りなく小さくなるのは、自然な性質

サンプル数nが多いと、p値が限りなく小さくなるのは、変な性質であったり、間違った計算をしているように見えることもありますが、 これ自体は正しいです。 標準誤差 の性質でもあります。 逐次学習 をすると、ある程度以上のサンプル数から、計算している値がほとんど変わらなくなりますが、その性質とも同じ物です。

サンプル数によって、P値が限りなく小さくなることが不自然な性質に見える場合は、平均値の差の検定ではなく、平均値の差の検定を評価方法として選択したところで間違っている可能性が高いです。

順路 次は 平均値の差の検定の仕組み