ちなみに、この分析は、 R-QCA1 でしています。
「こういう場合は、 平均値の差の検定 で検定する」と言わているようなケースで、実は、平均値の差の検定（正確には、t検定）が適していないことがあります。
統計的な検定と、統計教育の歴史 のページにあるように、2024年現在でも、あまり知られていない話ですが、P値を巡る混乱に巻き込まれないためには、重要な知識と、筆者は考えています。
「 平均値の差の検定 」、「 平均値の差の検定の、p値とサンプル数の関係 」、「 「平均値の数値的な差」というのは、どういうことですか？ 」、と言ったページでは、違う方向からこの話をしていますが、「できないこと」がわかりにくい説明になっています。 このページは、「できないこと」をシンプルに説明しようとしているページです。
できないことの典型的な例が、下のAとBの違いになります。
Aも、Bも、平均値の差は、約１です。 平均値の差の検定をすると、いずれも「有意な差」となります。
そのため、平均値の差の検定では、AとBを区別できないです。
言い方を変えると、「Bのように分布全体が重なり合っているのではなく、Aのようになっている」ということは、検証できないです。
さらに言い方を変えると、「データの分布に対して、平均値の差（例の場合は、１）が有意と言えるのか？」ということは、検証できないです。
つまり、多くの研究テーマにおいて検証したい事が、検証できないです。
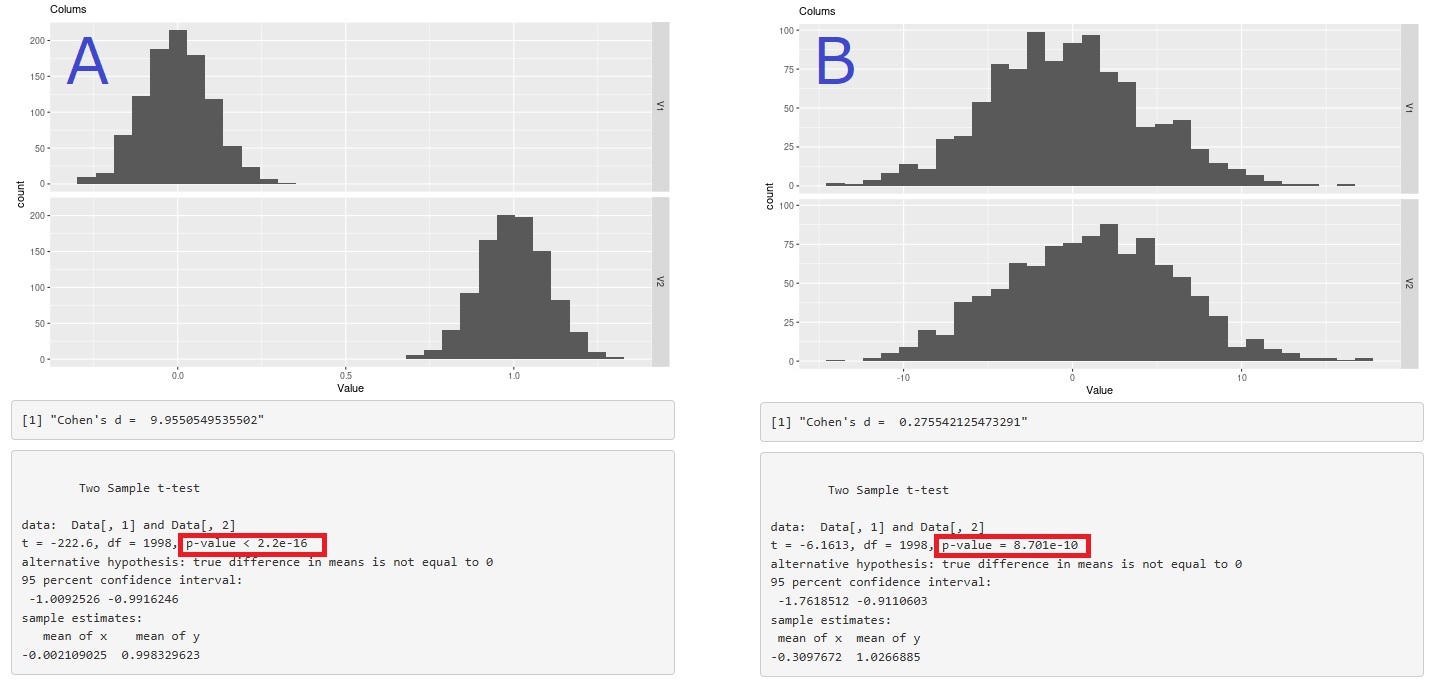
ちなみに、この分析は、
R-QCA1
でしています。
p値（p-value）は、Aが2.2e-16、Bが8.701e-10と出ています。
「e-16」というのは、例えば、「1.5e-2 = 0.015」という意味です。 分析結果では、e-16やe-10と出ているので、非常に小さい数であることがわかります。 なお、この分析で使っているRの場合、2.2e-16よりも小さな値は、「2.2e-16」と表示されるようなので、Aは、Rの限界を超えるほど小さい値なことがわかります。
AとBは、いずれも0.05よりも、はるかに小さな値です。 世の中でよく使われている、「p値は、0.05を基準に判断する」と考えると、AとBは、いずれも「有意差あり」となります。
平均値の差の検定では、「データの分布に対して、平均値の差が有意と言えるのか？」の評価ができないとしたら、「何を評価しているのか？」となりますが、 「平均値の数値的な差があるか？」を評価しています。
上のAとBについて、平均値の分布をグラフにすると、下のグラフのようになります。
程度の差はありますが、AもBも、２つの分布は、明確に分かれています。
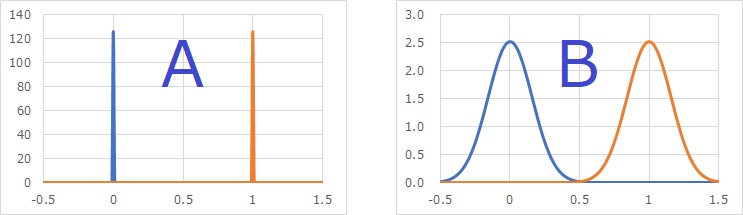
「平均値の数値的な差があるか？」という点では、AとBのいずれも「有意差あり」となったのは、正しい結果です。 AとBの平均値の差の分布の程度の差は、P値の大きさに表れています。 また、いずれも明確に分かれていることは、いずれも0.05よりもはるかに小さいことに表れています。 数値的な差の意味は、「 「平均値の数値的な差」というのは、どういうことですか？ 」のページにまとめています。
「データの分布に対して、平均値の差が有意と言えるのか？」の評価方法ですが、分布全体のずれを評価したいのなら、 データ全体の差の検定 があります。（ただし、知名度がとても低い方法です。）
ずれ以外も含めて、違いを評価したいのなら、 対応のない２標本の類似度分析 がありますが、こちらは使い勝手があまり良くないです。
話がややこしくなるのですが、サンプル数が10個以下くらいのスモールデータの場合は、平均値の差の検定で、p値0.05くらいを基準に判断した時に、 「２つの分布は、全体的に同じか？」と、「平均値の数値的な差があるか？」の両方について、評価ができます。
これができる理由は、「 スモールデータの検定の効果量 」のページにあります。
そのため、スモールデータの場合は、「２つの分布は、全体的に同じか？」の評価として、平均値の差の検定を使ったとしても、大きな間違いにはならないです。 ただし、「スモールデータの場合は、p値0.05くらいの時に、効果量が大きいので、大きな間違いにならない」という話なので、 「２つの分布は、全体的に同じか？」の評価は、別途、やっておいた方が良いです。
下の表は、 ノンパラメトリック検定 のページにあるものと同じです。
このページは、平均値の差の検定の話ですが、同様の性質は、下の表で、「数値のみ」と書いてある手法に共通しています。
順路
次は
効果量
