ビッグデータの統計学 のページにもありますが、ビッグデータに対して 検定 をする時は、判断基準として、p値(p value）はまったく役に立たず、 効果量が役に立ちます。
p値がn（データ量）の影響を受けやすい一方で、効果量にはそのような事がないのが理由です。
なお、ここでの「ビッグデータ」というのは、「万」や「億」の話ではなく、 検定のp値の問題は、100個以上くらいから深刻になっています。
工場では、５個（n=5）のグループを２つ用意するくらいの検定は、今でもよく行われています。 工場の場合、１個のデータを用意するだけでも、時間や費用が非常にかかることがあるためです。
その時は、「p値が0.05以下の時は、差があったと判断する」という昔ながらの方法が役に立ちます。
では、「工場で、『差がある』と判断している時に、効果量はどのくらいなのだろう？」という疑問がわきます。 そこで、調べてみました。
やり方は、手間がかかるものの簡単です。 乱数で、n=5のグループのデータを２組作り、それの平均値の差の検定をして、p値が0.049と0.050の間にある場合を片っ端から探しました。 工場では、「平均値は上がったと言えるか？」というような片側検定をすることが多いので、片側検定のp値です。 また、工場では、対応のない検定をする時が多いので、対応のない平均値の差の検定です。 n=5くらいだと、よほどでない限り、分散の違いを議論できないので、等分散を仮定した検定です。
下の図が、p値が0.049と0.050の間になる例になります。
「青が対策前、オレンジが対策後」のようなイメージです。
工場では、このようなデータになると、「対策の効果がある」と判断していることがわかります。
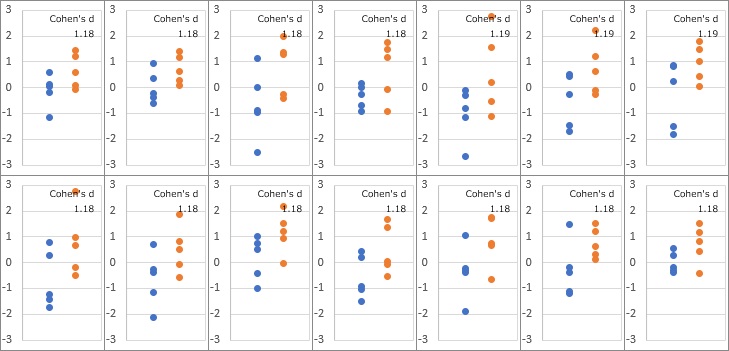
14通りありますが、効果量（コーエンのd）は、だいたい1.18でした。
世の中の目安としては、「0.8なら大きな効果」と考え、「0.2なら小さな効果」と考えるように言われていますが、 1.18程度でなければ「差がある」と判断しないということは、 それよりもかなり慎重に効果を判断していることになります。
スモールデータでp値が0.05を目安にするのは、悪くない目安です。 データが少ないので、これよりも甘くする（大きくする）のは危ないです。 世の中の目安のように、効果量を0.8と考えるということは、p値を0.05よりも大きくすることになります。
なお、 効果量の信頼区間のページでは、上記の考察よりもさらに深く、工場での目安を検証しています。
コーエンのdというのは、平均値の差を標準偏差で割った量です。 標準正規分布で考えるとわかりやすいと思うのですが、標準正規分布は、平均値が０で標準偏差が１です。
標準偏差が１同士の分布で平均値がずれると考えると、コーエンのdの分母は１になるので、平均値の差の大きさがそのままコーエンのdになります。
標準正規分布だと、-1から1の間に7割のサンプルが含まれます。 コーエンのdが1.18になるということは、その７割のサンプルの外の領域になるので、かなり明確に平均値がずれています。
上記では、n=5に固定して、p値が0.05くらいに限定して、効果量を調べています。
nの種類を増やし、p値の範囲も広げてグラフを作ると下のようになります。
（このグラフのp値は、両側検定です。）
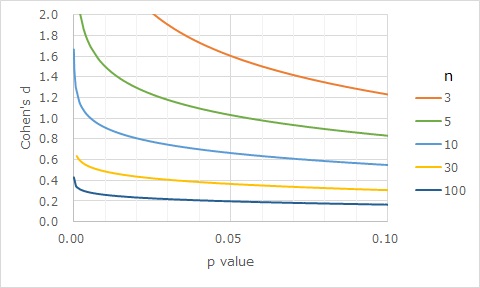
効果量が0.2を基準にするのでしたら、このグラフから、「p値が0.05以下」ということだけで、「平均値は十分な差がある」と考えられるのは、 n=100くらいまでということがわかります。 100を超えると、効果量が0.2よりも小さくても、p値が0.05以下になってしまうためです。 「安全を見るのなら、p値だけで判定できるのは、nが10個以内」と考えた方が良さそうです。
よって、効果量がある程度確保できるような平均値の差があることを検証する方法としては、 平均値の差の検定 のp値は、スモールデータの時にしか使えません。
順路
次は
ばらつきの違いの検定
