統計学 には、「データが多いことは、良いことだ」という話が昔からあります。
ところが、ビッグデータと呼ばれるような大量のデータには、この話がそのまま当てはまらないです。 このページでは、そうした事をまとめてみました。
なお、このページで、「データが多い」と言っているのは、 統計学の文献では、「サンプル数が多い」や、「n（エヌ）が多い」と言われます。 「サンプル」や「n」というと、統計学に慣れていない方には誤解の原因になるので、ここでは言い方を変えました。
平均値を知りたい場合、最低限必要なデータ数は、１個です。 ばらつきを知りたい場合、最低２個必要です。
ものすごく正確に測れていれば、これで充分です。 科学の世界では、１個のデータを取るだけでも大変なことがあり、 ものすごく注意して測っています。
しかし、一般的には、１個や２個のデータで出した結論は、不安な事が多いです。 そのため、データ数はできるだけ増やそうとします。 多ければ、精度が高くなります。 統計学の 推定 には、データ数が多いと精度が高くなるようになっている理論もあります。
今よりも、ずっと規模の小さなデータを扱っていた時代に、この理論は作られています。
「データ数が多い、少ない」という議論ですが、数個から数十個程度の範囲の話では、 データが少ない時代の理論で、特に問題はありません。 コンピュータによって、一度に扱えるデータ数が、数千、数万と増えて来て、 その時代には目立たなかった問題が、大きな問題になってきたようです。
ちなみに、数万くらいでは「ビッグデータ」と呼ばれないようです。 いわゆるビッグデータでは、下記の落とし穴が、もっとはっきりしているはずです。
統計学の 検定 の理論では、 「何かの違いを確認したい時は、P値0.05以下を目安にして、検定する。」と、説明されています。
ところが、この方法はビッグデータの時には使えません。
例えば、下の図は、
平均値の差の検定
の例です。
２つの分布の平均値の差は、約１です。これを検定すると、p値が2.2e-16（=0.00000000000000022）と書かれています。
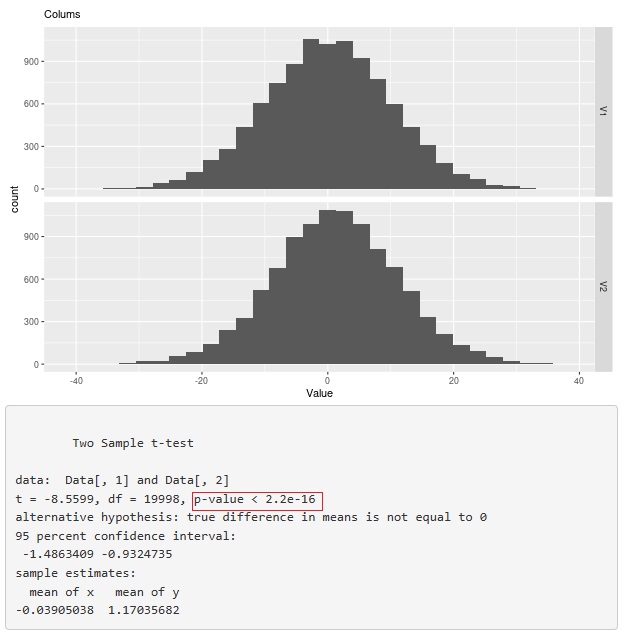
P値には、データ数が多いと、小さくなりやすい性質があります。 経験上、データ数が１万個位よりも大きな規模での検定では、この例のように、限りなくゼロに近いようなP値が見つかるのは、珍しくありません。
そして、このような解析結果は、何の役にも立たない事がほとんどです。 この例のデータが、対策の前後のデータだった場合に、「対策に効果があった」と言っても良いものでしょうか？ -40から40までの範囲でばらつくような現象について、「１」の改善が本当にあったとしても、現場感覚としては、「効果あり」とはならない事が多いです。 この現象から起こる現場の困り事には、変化が起きません。 また、ビジネスの実務で使うデータは、様々な誤差が影響しますし、この例のようなキレイな正規分布ではないことが普通なので、 -40から40までの範囲での「１」の違いというのは、「統計学的に扱えない種類の誤差」と考えると良いのではないかと思います。 （信頼区間に最小値がある統計学（統計学の不可能性））
P値の問題の直接的な対策は、 21世紀の検定 にあります。
データが多くて精度が高くなるのは、偶然誤差の部分です。 系統誤差は、依然として残っています。 系統誤差は、統計学ではどうしようもないことが原因なので、扱いの難しい誤差です。
昔ながらの統計学は、「一定条件で測定」が解析するデータの前提になっています。 このようなデータでは、 正規分布 がよく当てはまって、 検定 や 推定 の理論が威力を発揮します。
しかし、データ数が多い時は、「多様な条件で測定」になっていることが、よくあります。 このようなデータでも、統計ソフトに入れれば、何かしらの結果は出て来ますが、 前提が成り立っていないデータを使っていますので、その結果に素直に従ったら、どんな悪影響があるかわかりません。 これは、検定や推定の、もうひとつの落とし穴です。
「多様な条件で測定」したデータを、「一定条件で測定」したデータの形として使うには、 層別 のサンプリングが役に立つことがあります。 ただ、うまくデータを分類できないと、この方法は使えません。
データ数が少ない時は、グラフを見ても、差があるのかどうかが、よくわからないことが多いです。 グラフを見てもよくわからない時は、P値が頼りになります。
データ数が多い時は、P値を使わなくても、グラフを一目見れば、差の有無は一目瞭然の事がよくあります。 そのため、大量で多様なデータの解析では、P値は解析の主役になりにくいです。
大量で多様なデータを解析する時は、 散布図 ・ ヒストグラム ・ 折れ線グラフ といった初歩的なグラフが威力を発揮します。
また、このサイトでは、何かにつけては、 決定木 の考え方を推奨しています。 決定木は、多様な条件で測定したデータを、数値的に解析する方法のひとつです。
上記の 層別 の話と似ているのですが、ビッグデータと言っても、 層別（条件分け）をして、一部だけを取り出すと、その部分についてはデータ少ししかないことがあります。
データが少ししかない時には、昔ながらの統計学が威力を発揮します。
昔ながらの統計学の延長線上で、データが多いことの威力を説明しようとすると、 弱点も目立ってきます。 大量のデータがあっても、扱いが大変なだけで、あまり良い所がないような気もしてしまいます。
しかし、大量のデータを上手く見ることができると、 平均値や標準偏差といった統計手法では表現できないようなデータの特徴がわかることがあります。 これは、昔ながらの統計学の延長線上にはない威力です。 この辺りにも データサイエンス の面白さがあります。
センサーデータ は、数理モデルに当てはめる程度では、解析ができないデータの代表的なものです。
「ビッグデータ探偵団」 安宅和人・池宮伸次 著 講談社 2019
著者はYahoo!の方々で、ネット上のデータを分析してわかる「面白い」事実を紹介しています。
「データエコノミー入門 激変するマネー、銀行、企業」 野口悠紀雄 著 PHP研究所 2021
ビッグデータの時代の中で、最強のデータとして、マネーのデータを挙げています。
マネーのデータが作る未来と、諸問題を論じています。
順路
次は
統計分布
