上図は、ヒストグラムと確率密度関数です。 ヒストグラムは、平均値が０、標準偏差が１なので、その２つの値を使うと、確率密度関数が描けます。
平均値の差の検定 、 検定による判断 、 統計的な検定と、統計教育の歴史 、 21世紀の検定 といったページで、 「平均値の差の検定は、平均値の数値的な差の有無を調べる方法です。 しかし、一般的な調査や研究では、２つの分布の全体的な差を調べるのが目的で、平均値の数値的な差を調べたい訳ではないことが多いです。 こういう時は、手段（方法）と目的が合っていません。」という説明をしています。
ここで、「平均値の数値的な差」という意味は、 平均値の差の検定 と 標準誤差 のページで説明しているつもりですが、とてもわかりにくいようです。
できるだけシンプルに説明するのなら、以下の方が良いかもしれません。
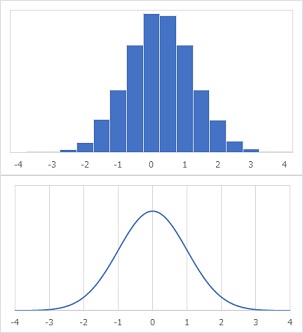
上図は、ヒストグラムと確率密度関数です。
ヒストグラムは、平均値が０、標準偏差が１なので、その２つの値を使うと、確率密度関数が描けます。
以下の説明は、確率密度関数のグラフを使います。
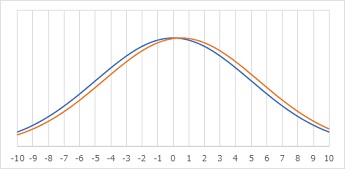
まず、上のグラフでは、確率密度関数が２つあります。
中心は、0と0.5で違うようですが、この場合は、「２つは、かなり重なる。実務的には、『同じ』と思った方が良さそう。」となります。
次に下のグラフの場合は、中心は、0と0.5で上の場合と同じようですが、針のような分布になっていて、重なっている部分がほとんどありません。
この場合は、「２つは、異なる。」となります。
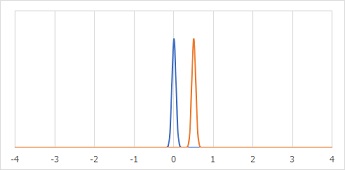
平均値の差の検定 では、このようなグラフの考え方で評価しているものが平均値の分布です。 平均値を計算するのに使ったデータの分布では、ありません。
「説明の準備」のところで、ヒストグラムと確率密度関数を説明しています。 確率密度関数は、ヒストグラムを滑らかな曲線に近似した曲線としての意味があります。 データから直接作るヒストグラムと、データの平均値と標準偏差から作る確率密度関数には、このような関係があります。
では、平均値の分布を表す確率密度関数と、ほぼ同じ形をした平均値のヒストグラムがあるかというと、ありません。
標準誤差 の求め方になって来るのですが、平均値の分布を表す確率密度関数は、データの平均値、データの標準偏差、サンプル数から求まる関数になっています。
確率密度関数自体に使うのは、平均値と標準偏差ですが、平均値の分布の場合、この平均値に使うのは、データの平均値です。 標準偏差に相当するのは、データの標準偏差ではなく、 標準誤差 （データの標準偏差を、サンプル数の平方根で割った値）になります。 サンプル数の平方根で割っているので、平均値の分布のばらつきは、元のデータのばらつきよりも狭くなります。
「平均値の分布」と書くと、 ベイズ統計 を知っている方からは、「頻度論で平均値に分布はない」という指摘をいただきそうです。
適切な表現があれば、改めますが、上のようなグラフは、 標準誤差 の考え方から出て来るものなので、「平均値の分布」と呼んでも良いと筆者は考えています。 ただし、ベイズ統計的な「平均値の分布」と、異なっていることは、筆者も認識しています。
この点については、 統計量の分布 のページにまとめています。
上の２つの例ですが、２つの分布がほとんど重なっている場合も、針のような分布の場合も、平均値を計算すると、約0.0と、約0.5になります。
平均値の分布がわかると、この平均値の確からしさがわかります。
ほとんど重なるような場合は、計算した平均値が約0.0になっていても、真の平均値は、-8や5といった値にもなる可能性を表現しています。 ２つの確率密度関数の両方がそんな状態なので、「実務的には、『同じ』と思った方が良さそう。」という解釈になってきます。
針のような分布の場合は、計算した平均値が約0.0なら、真の値も、0.0にかなりの精度で近いと考えられます。 0.5になるとは、非常に考えにくいです。 計算した平均値が約0.5の場合も同様です。 そのため、「２つは、異なる。」という解釈になります。
平均値を計算して、0.0と0.5だったとしても、平均値の分布がほとんど重なる場合は、「数値的な差はない」と考えられます。 より正確に言うのなら、「数値的な差があるとは、考えにくい」という言い方の方が適切かもしれません。
平均値の分布が針のようになっていて、ほとんど重ならない場合は、「数値的な差はある」と考えられます。
「0.0と0.5」というと、差があるようにも見えますが、平均値の分布を見ると、確からしさを考慮できるようになります。 実務で数字を扱う中では、とてもありがたい理論です。
冒頭の話に戻ると、平均値の差の検定は、こういうことを調べている方法です。 つまり、平均値の差の検定は、「数値的な差があるのか」を調べる方法です。
標準誤差は、元のデータの標準偏差と、サンプル数で決まるものですが、サンプル数が多いと、サンプル数で、ほとんど決まるような尺度です。
サンプル数が多いと、元のデータの標準偏差は、ほとんど関係なくなるため、データ全体の違いを調べる方法にはならないです。 特に、「元のデータの分布に対して、計算した平均値の確からしさは、どの程度か？」ということを調べる理論にはなっていない点がポイントです。
