２種類の対立仮説

このページは、αとβの説明でよく使われる図と、対立仮説の言葉による説明が合っていない解説が、世の中では多い事に気付き、筆者なりにまとめてみたものです。

ネイマン・ピアソン流の検定では、帰無仮説と対立仮説の２つが出て来ます。

フィッシャー流と、ネイマン・ピアソン流の混同の一番わかりやすいところが、これらの仮説の考え方です。混同された結果、現在は、対立仮説の定義が、世の中で２種類あります。

「対立仮説とは、帰無仮説と論理的に逆のもの」の場合

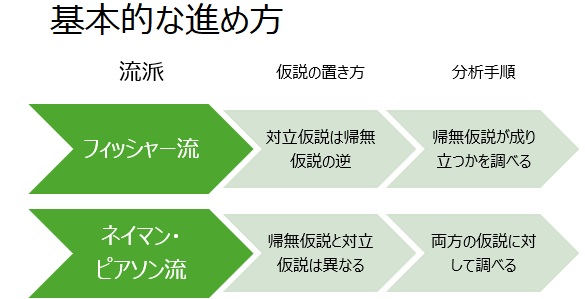
フィッシャー流の検定をする時の、対立仮説の考え方です。

「対立仮説とは、帰無仮説と論理的に逆のもの」の場合、例えば、以下のようにして仮説を設定します。いずれも、帰無仮説と対立仮説は、論理的に逆な関係になっています。

「対立仮説とは、帰無仮説と論理的に逆のもの」と考えている場合、まず、帰無仮説が正しいかどうかを調べます。帰無仮説が否定されると、対立仮説が正しいことになります。

なお、論理的に逆なものは、どんなものでも仮説にできるほど、検定は万能ではないです。この進め方をする場合、帰無仮説と対立仮説の関係と、選んだ検定手法が、きちんと結び付いている必要があります。

上記の例の場合、「平均値の検定の、両側検定」、「平均値の差の検定（両側検定、または、片側検定）」がそれぞれ当てはまります。

以下のような対立仮説の場合、これは、論理的に逆でないですが、この場合も、フィッシャー流です。

この例の場合は、「平均値の検定の、片側検定」が当てはまります。

ネイマン・ピアソン流では、「対立仮説と、帰無仮説は、それぞれが分布」と考えています。

「対立仮説と、帰無仮説は、それぞれが分布」の場合、例えば、以下のようにして仮説を設定します。

「対立仮説とは、帰無仮説と論理的に逆のもの」では、帰無仮説が否定されると、対立仮説が成り立ちます。

しかし、分布が２つある場合、帰無仮説が否定されたからといって、直ちに対立仮説が肯定される理論にはなっていません。

極端な例ですが、下のような場合のように、「帰無仮説と対立仮説の両方が否定される」という結論もあり得なくはないです。

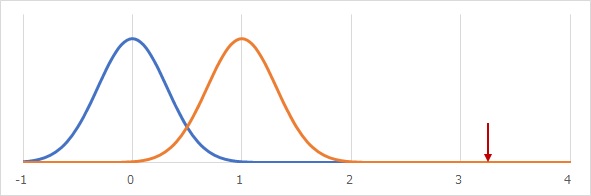
分布が２つある場合、帰無仮説が否定されたからといって、直ちに対立仮説が肯定される理論にはなっていないです。

ところが、フィッシャー流と、ネイマン・ピアソン流を混同していると、分布が２つある場合にも、帰無仮説の否定は、対立仮説の肯定を意味するものと誤解してしまいます。