21世紀の検定 としての、 分散分析 を、このページで整理します。
分散分析は、２つ以上のグループを比較するための方法です。 分散分析で２つのグループを対象にした場合と、平均値の差の検定をした場合は、結果が同じになります。 ２つのグループを対象にする場合は、分散分析よりも、 21世紀の、平均値の差の検定 を使った方が、いろいろなことが調べられます。
このページでは、３つのグループがある場合を想定して説明しています。
他の検定の説明では、指標の計算方法を個別に説明していましたが、分散分析は、表を作りながら途中の計算をするので、
計算式は、冒頭に図で説明します。
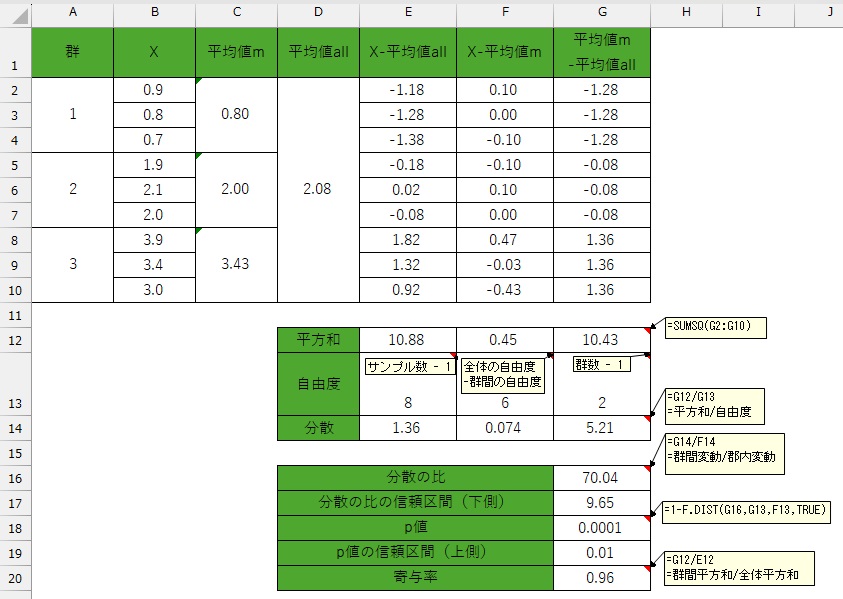
検定の対象は、分散の比です。
分散の比の検定 では、分子と分母が、２つのグループのそれぞれの分散ですが、分散分析では、分子が平均値の分散、分母が誤差の分散です。 分散の比を使う分析ですが、平均値の違いを調べる方法として作られています。
以下では、 分散の比の検定 のページと異なる点だけを説明します。
基本的に 分散の比の検定 と同じです。 ただし、分散の比の検定のページでは、「分散は小さくなったと言えるか？」ということを調べようとして、分散の比が１よりも小さい場合を評価しています。 一方、このページは、「平均値の分散は、大きいのか？」ということを調べようとして、分散の比が１よりも大きい場合を評価しています。
この点が、F.DIST関数の使い方の違いになっています。
分散の比の検定 では、２つのグループの分散を比較するので、寄与率は、分散の比から定義しています。
分散分析の場合は、 平均値の差の検定の寄与率 と同じ考え方で寄与率が定義できます。
ただし、平均値が３つ以上ある場合は、相関係数を使って寄与率を求める方法は使えないので、群間平方和と全体平方和から計算します。
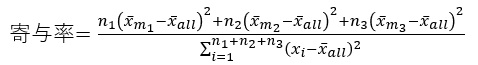
分散の比の検定では、分散の比で寄与率を定義したので、分散の比の信頼区間から、 寄与率の信頼区間 を求めています。
平均値の差の検定では、相関係数で寄与率を求めるので、相関係数の信頼区間から、 寄与率の信頼区間 を求めています。
分散分析の寄与率の信頼区間については、どちらの方法も当てはまらないので、今のところ、計算方法が思い当たりません。
順路
次は
21世紀の、比率の差の検定
