まず、ここでは、上のようなデータがあったとします。 左がヒストグラム、右はデータを元にして、正規分布で近似した曲線です。 そして、「帰無仮説を０とした時に、データの平均値は０と言えるか？」を検定したいとします。
P値の問題点への対策として、 信頼区間 が挙げられることがあります。
信頼区間を見ると、P値だけからはわからないことが分析できるようになります。
「サンプル数が大きいと、P値は小さくなりやすい」というP値の特徴は、 信頼区間では、「サンプル数が大きいと、信頼区間が狭くなりやすい」という特徴になっているので、P値の問題点として言われていることへの対策にはならないです。
このページは、その理由を説明します。
以下は、 平均値の検定 を例にしていますが、他の検定でも同様です。
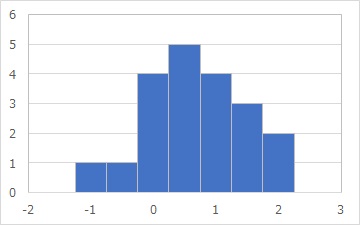
まず、ここでは、上のようなデータがあったとします。
左がヒストグラム、右はデータを元にして、正規分布で近似した曲線です。
そして、「帰無仮説を０とした時に、データの平均値は０と言えるか？」を検定したいとします。
次の手順で、平均値の分布を調べます。
標準偏差ではなく、標準誤差がばらつきの大きさになるので、元のデータよりも範囲が狭まります。
このデータは、サンプル数が10個なので、標準偏差を10の平方根で割った値が、標準誤差です。
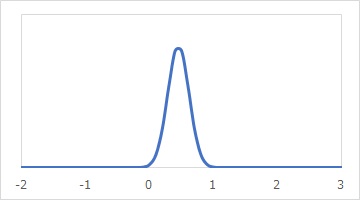
上の統計量の分布のグラフの横軸を広げて、見やすくしてから、95%信頼区間を書き込むと、以下になります。
95%信頼区間の外側は、上側と下側がありますが、それぞれ2.5%（= 5% / 2）ずつあります。
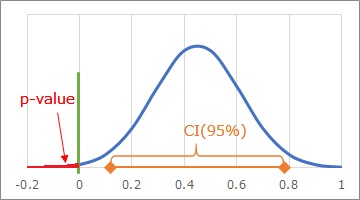
この場合は、信頼区間が０を含んでいるので、「平均値は0.638だが、真の平均値が０という可能性が否定できない」という結果になります。
下のグラフは、中心が０です。分布の標準偏差は、平均値の分布と同じです。
p値は、ピンクの部分の面積です。分布全体を１とすると、ピンクの部分の面積は、0.031です。これがp値です。
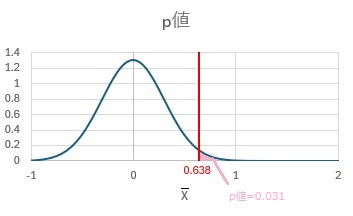
p値の計算では、「真の平均値を０と仮定した場合に、0.638の位置は？」という見方をするので、０を中心とした分布で計算します。
ところで、以下のようにして、0.638を中心とした分布についての、0以下の面積も同じです。
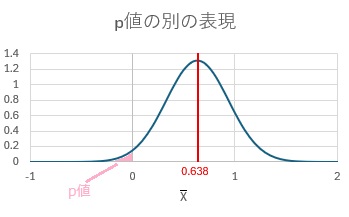
上記のグラフをまとめると、以下のようになります。
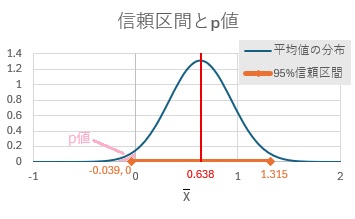
p値は、ピンクの部分の面積で、0.031です。両側検定では、0.062（= 0.031*2）です。 一方、信頼区間の下側よりも外側の面積は、0.025（2.5%）です。
確率の単位で見るか、変数の単位で見るかの違いはありますが、どちらのアプローチでも、結果は変わりません。
信頼区間は、仮説がいくつなのかは関係なく、統計量の分布だけから求まります。 統計量の分布は、データだけから求まります。
P値は、統計量の分布だけでなく、仮説の数字もあると求まります。
信頼区間には、データだけから求まることを把握する指標としての使い方があります。
次は
P値の信頼区間
