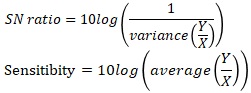
There are two relatively new signal-to-noise ratios: energy ratio type and variation ratio type. The names are different, but the content seems to be the same. "Energy" is the "Energy" of Quality Engineering, not in the physical sense.
In the energy ratio type and fluctuation ratio type, the total variation (sum of Y squares) is divided into a part that can be explained by the model and a part of error.
Then, let the SN ratio as log of
the part that can be explained by
the modelo / error part
The energy ratio type also includes ideas to eliminate the influence of n (number of samples). Taking the coefficient of variation as an example, in the calculation, the average value of the denominator is divided by n, and the standard deviation of the numerator is divided by n-1, so even if they have exactly the same variation, The way n is taken affects the coefficient of variation.
The same situation applies to the calculation formula with correction. In the energy ratio type idea, we think that "this is not possible to compare experiments with different n values", so we calculate it so as to eliminate the part divided by n and n-1. (By the way, "replacing the part divided by n-1 with n" means the same thing.)
In general statistics, variance is divided by n-1 because we think that Unbiased Variance should be used. In the calculation of the energy ratio type, divide by n. We are moving away from discussing variance estimators and looking at the data in a way that prioritizes computational simplicity.
When the part that can be explained by the model / the error part is the part, the idea of "combining n" is also included.
The square of the correlation coefficient is called the coefficient of determination or the contribution factor. It is called the contribution factor because the square of the
correlation coefficient = the partial variation that can be explained by the model / total variation.
Total variation = part that can be explained by the model + part of error Since the correlation coefficient
and the SN Rratio of the dynamic characteristics of the energy ratio type are similar in analysis.
Quality engineering often deals with Proportional variance. The general Dynamic SN Ratio is an analogy from the Static SN Ratio, and seems to have been created with the idea of "dividing the slope by the error variance". In particular, the mathematical expression of proportional variance is not conscious.
The SN ratio of the dynamic characteristics of the energy ratio type / fluctuation ratio type and the SN ratio for proportional dispersion below have a meaning as a mathematical expression of proportional variance, but as you can see on the SN ratio of dynamic characteristics page, the characteristics they measure are not the same.
There is a literature that states that the SNR ratio of the dynamic characteristics of the energy ratio type and the fluctuation ratio type applies to the mathematical expression of proportional variance.
As I wrote in Quality Engineering Approach to Proportional variance, In my opinion, the following signal-to-noise ratios can also be used for proportional dispersion.
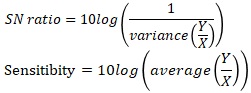
In quality engineering, "X" is often written as "M". Variance is variance and average is average. In quality engineering, the words "variance" and "average" are often used directly.
In the case of SNR ratios for proportional variance, the ratio is calculated at all levels before all levels are treated, so all levels are treated equally. The influence of the signal (X) on a larger level does not increase.
On the SN ratio page for static characteristics, we write "(Y mean value / Y standard deviation) squared" in the SN ratio of the desirable characteristic.
In a typical reference, this part is written as
(Sm /n)/ VE
, or a further modified version of the equation.
(Y mean / Y standard deviation) squared = (Sm /n)/Ve
, so it looks different, but the content is the same.
Ve is the same as unbiased variance:
Ve = Se / (n-1).
Here, if the part of
(Sm /n)/ ve
is (Sm /n)/
(Se /n)
,
it becomes an energy ratio type.
(Sm /n)/ (Se /n)= Sm/Se
.
St = sum of squares of Y
and
St = Sm + Se
, so the SN ratio of the desirability characteristic of the energy ratio type has the meaning as the ratio of the decomposition of the sum of squares. It is not simply a change of n-1 to n.
NEXT 

 Classification of factors
Classification of factors
