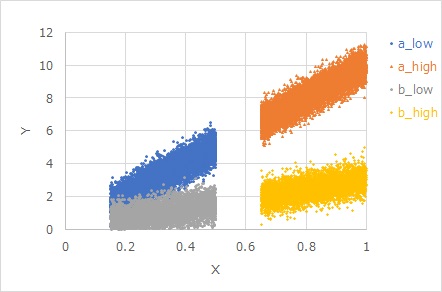
Equal variance is a case where Y increases in proportion to X, but the variation of Y when the value of X is the same can be assumed to be constant. It is an image that there is a distribution on a band of constant thickness.
In quality engineering , "characteristics" means the characteristics expected for Y.
The definition of SN ratio is different to consider characteristics of Y. It depends on the kinds of characteristics.
In static characteristics, Y is expected as fixed.
A dynamic characteristic is a characteristic in which Y changes depending on X (signal factor). In practical terms, by changing X, This is the case when the quality is such that Y also changes. For example, the quality of a car's brakes is its dynamic characteristics. This is related to the amount of pressure (X) and the degree of braking (Y).
"Good dynamic characteristics" means that even if the value of X changes, For each X value, it is said that the expected Y value can be reliably obtained. In the example of the brake, even if you step on it in the same way, the effect of the brake will be It would be dangerous if it was different at that time, so a reliable numerical relationship between X and Y is desired. In the experiment of dynamic characteristics, In the combination condition of the control factor and the error factor, Look for conditions with "good dynamic characteristics".
In the quality engineering literature, there are sometimes three types of dynamic characteristics.
The author divided it into 8 types as follows. There are 8 types in 2 * 2 * 2. It is divided into two types according to "equal dispersion and proportional dispersion". There are two types of variance: whether the variance is proportional to the slope or not. There are two types of "origin is not a standard / standard".
As for how to read the graph below, assuming each characteristic, the four groups in the figure have the same magnitude of variation.

Equal variance is a case where Y increases in proportion to X, but the variation of Y when the value of X is the same can be assumed to be constant. It is an image that there is a distribution on a band of constant thickness.
"The variance is not proportional to the slope" is when it is considered natural that the length of the bands in the Y-axis direction is constant when there are two distributions of different slopes.
In the sense of equal variance characteristic 1, the four groups in the above figure are considered to have the same magnitude of variation.
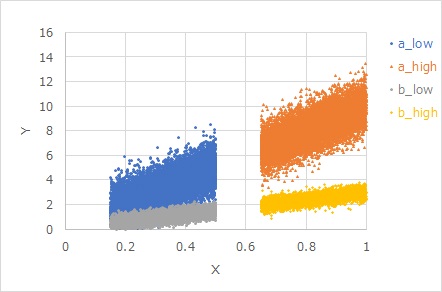
Even with the same equal variance, if the variance is proportional to the slope, it is natural that if the slope is doubled, the width of the band will also double.
In appearance, even if the width of the band appears to be narrower if the slope is slower, if the property is that the dispersion is proportional to the slope, the magnitude of the variation may be the same.
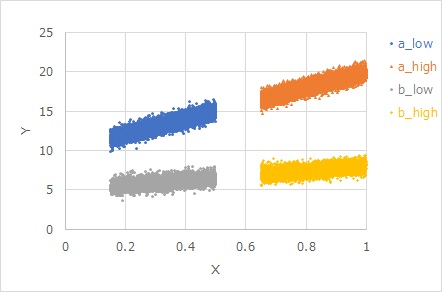
It is an application of the uniform dispersion characteristic 1. In the uniform variance characteristic, "the origin is not the standard" is a case where the origin does not pass.

This is the case where the application of the uniform dispersion characteristic 2 does not pass through the origin.
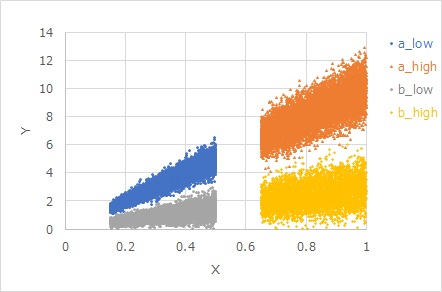
"Proportional dispersion" is a term coined by the author. Unlike equal variance, the magnitude of the variation changes in proportion to X. On this site, we call it "proportional distribution".
"The variance is not proportional to the slope" is when it is considered natural that the variation of the two distributions is the same if there are two distributions with different slopes, and the same X is the same.
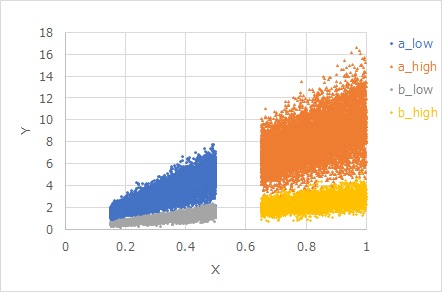
As with the uniform variance characteristic 2, the proportional dispersion characteristic may also have a dispersion proportional to the slope. On this site, you will find the I call it the "proportional proportional distribution model."
Proportional variance characteristics 3 and 4 correspond to cases where the origin is not a reference, with proportional variance characteristics 1 and 2.
However, since proportional variance has an intrinsic meaning of spreading dispersion from the origin, it is difficult to think of a physical phenomenon that spreads from a point other than the origin.
NEXT 

 Difference of Static and Dynamic
Difference of Static and Dynamic
