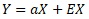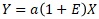The "a+E" part of Proportional variance model can be interpreted as "the variation in which the mean value is a". If you think about it that way, a and E represent two things in one. The proportional variance model is a multiplicative model (a multiplicative model in a broad sense) in which "a + E" and X are multiplied.
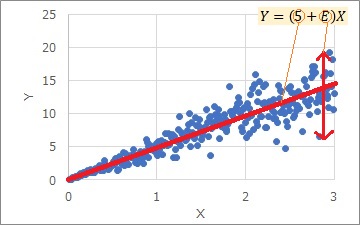
The graph above is an example of a proportional distribution model.
In the proportional variance model, the a part is the slope, and the E part is a number that determines the magnitude of the variation in the Y-axis direction.
The proportional distribution model can be expressed by the equation , but
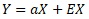
it is convenient to interpret it as a model that combines the two effects of aX and EX, because it allows you to consider countermeasures separately.
A model that can be expressed as a multiplicative model in this way, but can be written like an additive model and interpreted like an additive model, is called an "additive model multiplicative model" here.
Of the chance errors and systematic errors, the chance error is a distribution with a mean value of 0, and the systematic error is a deviation from the mean value.
The fact that the "a + E" part is considered to be "the variation in which the mean value is a" can be interpreted as "both chance error and systematic error are included".
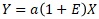
If you write it in the form of, Proportional-proportional variance model is also a multiplicative model.
However, "1" is used for convenience in order to make it a form of a multiplicative model. It doesn't have any particular physical meaning. This is different from the proportional distribution model. Therefore, as a model formula, it feels unnatural.
